Introducción
Una técnica estadística confiable para determinar la significancia es el análisis de varianza (ANOVA), especialmente cuando se comparan más de dos promedios muestrales. Aunque la distribución t es adecuada para comparar las medias de dos muestras, se requiere un ANOVA cuando se trabaja con tres o más muestras a la vez para determinar si sus medias son las mismas, ya que provienen de la misma población subyacente.
Por ejemplo, se puede utilizar ANOVA para determinar si diferentes fertilizantes tienen diferentes efectos sobre la producción de trigo en diferentes parcelas y si estos tratamientos proporcionan resultados estadísticamente diferentes para la misma población.

El Prof. RA Fisher introdujo el término "Análisis de Varianza" en 1920 al abordar el problema del análisis de datos agronómicos. La variabilidad es una característica fundamental de los eventos naturales. La variación general en cualquier conjunto de datos se origina en múltiples fuentes, que pueden clasificarse en términos generales como causas asignables y casuales.
La variación debida a causas asignables se puede detectar y medir, mientras que la variación debida a causas casuales está más allá del control de la mano humana y no se puede tratar por separado.
Según RA Fisher, el Análisis de Varianza (ANOVA) es la “Separación de la Varianza atribuible a un grupo de causas de la varianza atribuible a otro grupo”.
OBJETIVOS DE APRENDIZAJE
- Comprender el concepto de Análisis de Varianza (ANOVA) y su importancia en el análisis estadístico, particularmente al comparar promedios de múltiples muestras.
- Conozca los supuestos necesarios para realizar una prueba ANOVA y su aplicación en diferentes campos como la medicina, la educación, el marketing, la fabricación, la psicología y la agricultura.
- Explore el proceso paso a paso de realizar un ANOVA unidireccional, incluido el establecimiento de hipótesis nulas y alternativas, la recopilación y organización de datos, el cálculo de estadísticas de grupo, la determinación de la suma de cuadrados, el cálculo de grados de libertad y el cálculo de cuadrados medios. , cálculo de estadísticas F, determinación del valor crítico y toma de decisiones.
- Obtenga información práctica sobre la implementación de una prueba ANOVA unidireccional en Python utilizando la biblioteca scipy.stats.
- Comprender el nivel de significancia y la interpretación del estadístico F y el valor p en el contexto de ANOVA.
- Conozca los métodos de análisis post-hoc como la diferencia honestamente significativa (HSD) de Tukey para un análisis más detallado de las diferencias significativas entre grupos.
Tabla de contenidos.
Supuestos para la PRUEBA ANOVA
La prueba ANOVA se basa en las estadísticas de prueba F.
Las suposiciones hechas con respecto a la validez de la prueba F en ANOVA incluyen las siguientes:
- Las observaciones son independientes.
- La población principal de la que se toman las observaciones es normal.
- Varios tratamientos y efectos ambientales son de naturaleza aditiva.
ANOVA unidireccional
ANOVA unidireccional es un prueba estadistica Se utiliza para determinar si existen diferencias estadísticamente significativas en las medias de tres o más grupos para un solo factor (variable independiente). Compara la varianza entre grupos con la varianza dentro de los grupos para evaluar si estas diferencias probablemente se deben al azar o a un efecto sistemático del factor.
Varios casos de uso de ANOVA unidireccional de diferentes dominios son:
- Medicina: Se puede utilizar ANOVA unidireccional para comparar la efectividad de diferentes tratamientos en una afección médica particular. Por ejemplo, podría usarse para determinar si tres medicamentos diferentes tienen efectos significativamente diferentes para reducir la presión arterial.
- EDUCACION: Se puede utilizar ANOVA unidireccional para analizar si existen diferencias significativas en las puntuaciones de las pruebas entre los estudiantes a quienes se les ha enseñado utilizando diferentes métodos de enseñanza.
- Márketing: Se puede emplear ANOVA unidireccional para evaluar si existen diferencias significativas en los niveles de satisfacción del cliente entre productos de diferentes marcas.
- Fabricación: Se puede utilizar ANOVA unidireccional para analizar si existen diferencias significativas en la resistencia de los materiales producidos por diferentes procesos de fabricación.
- Psicología: Se puede utilizar ANOVA unidireccional para investigar si existen diferencias significativas en los niveles de ansiedad entre los participantes expuestos a diferentes factores estresantes.
- Agricultura: Se puede utilizar ANOVA unidireccional para determinar si diferentes fertilizantes conducen a rendimientos de cultivos significativamente diferentes en experimentos agrícolas.
Entendamos esto con el ejemplo de Agricultura en detalle:
En la investigación agrícola, se puede emplear ANOVA unidireccional para evaluar si diferentes fertilizantes conducen a rendimientos de cultivos significativamente diferentes.
Efecto de los fertilizantes sobre el crecimiento de las plantas
Imagine que está investigando el impacto de diferentes fertilizantes en el crecimiento de las plantas. Se aplican tres tipos de fertilizantes (A, B y C) para separar grupos de plantas. Después de un período determinado, se mide la altura promedio de las plantas en cada grupo. Puedes utilizar ANOVA unidireccional para probar si hay una diferencia significativa en la altura promedio entre las plantas cultivadas con diferentes fertilizantes.
Paso 1: Hipótesis nulas y alternativas
El primer paso es intensificar las hipótesis nulas y alternativas:
- Hipótesis nula (H0): Las medias de todos los grupos son iguales (no hay diferencia significativa en el crecimiento de las plantas debido al tipo de fertilizante)
- Hipótesis alternativa (H1): Al menos una media de grupo es diferente de los demás (el tipo de fertilizante tiene un efecto significativo en el crecimiento de las plantas).
Paso 2: recopilación y organización de datos
Después de un período de crecimiento determinado, mida cuidadosamente la altura final de cada planta en los tres grupos. Ahora organiza tus datos. Cada columna representa un tipo de fertilizante (A, B, C) y cada fila contiene la altura de una planta individual dentro de ese grupo.
Paso 3: Calcular las estadísticas del grupo.
- Calcule la altura final media de las plantas en cada grupo de fertilizantes (A, B y C).
- Calcule el número total de plantas observadas (N) en todos los grupos.
- Determine el número total de grupos (K) en nuestro caso, k=3(A, B, C)
Paso 4: Calcular la suma de los cuadrados
Por lo tanto, se calculará la suma total del cuadrado, la suma del cuadrado entre grupos y la suma del cuadrado dentro del grupo.
Aquí, la suma total de cuadrados representa la variación total en la altura final de todas las plantas.
La suma de cuadrados entre grupos refleja la variación observada entre las alturas promedio de los tres grupos de fertilizantes. Y la suma de cuadrados dentro del grupo captura la variación en las alturas finales dentro de cada grupo de fertilizantes.
Paso 5: Calcular los grados de libertad
Los grados de libertad definen el número de piezas de información independientes utilizadas para estimar un parámetro de población.
- Grados de libertad entre grupos: k-1 (número de grupos menos 1) Entonces, aquí será 3-1 =2
- Grados de libertad dentro del grupo: Nk (Número total de observaciones menos número de grupos)
Paso 6: Calcular los cuadrados medios
La media de cuadrados se obtiene dividiendo la respectiva Suma de Cuadrados por grados de libertad.
- Cuadrático medio entre: Entre grupos Suma de cuadrados/Grados de libertad Entre grupos
- Media cuadrática interior: Suma de cuadrados/grados de libertad dentro del grupo dentro del grupo
Paso 7: Calcular las estadísticas F
La estadística F es una estadística de prueba que se utiliza para comparar la variación entre grupos con la variación dentro de los grupos. Una estadística F más alta sugiere un efecto potencialmente más fuerte del tipo de fertilizante sobre el crecimiento de las plantas.
El estadístico F para Anova unidireccional se calcula utilizando esta fórmula:
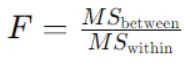
Aquí,
MSbetween es el cuadrado medio entre grupos, calculado como la suma de cuadrados entre grupos dividida por los grados de libertad entre grupos.
MSwithin es el cuadrado medio dentro de los grupos, calculado como la suma de los cuadrados dentro de los grupos dividida por los grados de libertad dentro de los grupos.
- Grados de libertad entre grupos (dof_between): dof_entre = k-1
Donde k es el número de grupos (niveles) de la variable independiente.
- Grados de libertad dentro de grupos (dof_within): dof_within = Nk
Donde N es el número de observaciones y k es el número de grupos (niveles) de la variable independiente.
Para ANOVA unidireccional, los grados de libertad totales son la suma de los grados de libertad entre grupos y dentro de los grupos:
dof_total= dof_entre+dof_dentro
Paso 8: Determinar el valor crítico y la decisión
Elija un nivel de significancia (alfa) para el análisis, normalmente se elige 0.05
Busque el valor F crítico en el nivel alfa elegido y los grados de libertad entre grupos y los grados de libertad dentro del grupo calculados utilizando una tabla de distribución F.
Compare el estadístico F calculado con el valor F crítico
- Si el estadístico F calculado es mayor que el valor F crítico, rechace la hipótesis nula (H0). Esto indica una diferencia estadísticamente significativa en la altura promedio de las plantas entre los tres grupos de fertilizantes.
- Si el estadístico F calculado es menor o igual que el valor F crítico, no se rechaza la hipótesis nula (H0). No se puede concluir una diferencia significativa basándose en estos datos.
Paso 9: Análisis post-hoc (si es necesario)
Si hipótesis nula es rechazado, lo que significa una diferencia general significativa, es posible que desee profundizar más. Post-hoc como la diferencia honestamente significativa (HSD) de Tukey puede ayudar a identificar qué grupos de fertilizantes específicos tienen alturas promedio de plantas estadísticamente diferentes.
Implementación en Python:
import scipy.stats as stats
# Sample plant height data for each fertilizer type
plant_heights_A = [25, 28, 23, 27, 26]
plant_heights_B = [20, 22, 19, 21, 24]
plant_heights_C = [18, 20, 17, 19, 21]
# Perform one-way ANOVA
f_value, p_value = stats.f_oneway(plant_heights_A, plant_heights_B, plant_heights_C)
# Interpretation
print("F-statistic:", f_value)
print("p-value:", p_value)
# Significance level (alpha) - typically set at 0.05
alpha = 0.05
if p_value < alpha:
print("Reject H0: There is a significant difference in plant growth between the fertilizer groups.")
else:
print("Fail to reject H0: We cannot conclude a significant difference based on this sample.")
Salida:

El grado de libertad entre ellos es K-1 = 3-1 =2, donde k representa el número de grupos de fertilizantes. El grado de libertad interno es Nk = 15-3 = 12, donde N representa el número total de puntos de datos.
F-crítico a dof(2,12) se puede calcular a partir de F-Mesa de distribución a un nivel de significación de 0.05.
F-crítico = 9.42
Dado que F-Crítico < F-estadístico, rechazamos la hipótesis nula que concluye que existe una diferencia significativa en el crecimiento de las plantas entre los grupos de fertilizantes.
Con un valor p inferior a 0.05, nuestra conclusión sigue siendo consistente: rechazamos la hipótesis nula, lo que indica una diferencia significativa en el crecimiento de las plantas entre los grupos de fertilizantes.
ANOVA bidireccional
El ANOVA unidireccional es adecuado solo para un factor, pero ¿qué pasa si tienes dos factores que influyen en tu experimento? Luego se utiliza ANOVA de dos vías que le permite analizar los efectos de dos variables independientes en una única variable dependiente.
Paso 1: establecer hipótesis
- Hipótesis nula (H0): No hay una diferencia significativa en la altura promedio final de la planta debido al tipo de fertilizante (A, B, C) o al momento de siembra (temprana, tardía) o su interacción.
- Hipótesis alternativa (H1): Al menos uno de los siguientes es cierto:
- El tipo de fertilizante tiene un efecto significativo sobre la altura final promedio.
- El tiempo de siembra tiene un efecto significativo en la altura final promedio.
- Existe un efecto de interacción significativo entre el tipo de fertilizante y el momento de la siembra. Esto significa que el efecto de un factor (fertilizante) depende del nivel del otro factor (época de siembra).
Paso 2: recopilación y organización de datos
- Mida las alturas finales de las plantas.
- Organice sus datos en una tabla con filas que representen plantas individuales y columnas para:
- Tipo de fertilizante (A, B, C)
- Época de siembra (temprana, tardía)
- Altura final (cm)
Aquí está la tabla:

Paso 3: Calcular la suma de los cuadrados
De manera similar al ANOVA unidireccional, tendrás que calcular varias sumas de cuadrados para evaluar la variación en las alturas finales:
- Suma Total de Cuadrados (SST): Representa la variación total entre todas las plantas. Suma de cuadrados del efecto principal:
- Tipos entre fertilizantes (SSB_F): Refleja la variación debida a diferencias en el tipo de fertilizante (promediado según las épocas de siembra)
- Tiempos entre revestimientos (SSB_T): Refleja la variación debida a las diferencias en las épocas de siembra (promediada entre tipos de fertilizantes).
- Suma de cuadrados de interacción (SSI): Capta la variación debida a la interacción entre el tipo de fertilizante y el momento de siembra.
- Suma de cuadrados dentro del grupo (SSW): Representa la variación en las alturas finales dentro de cada combinación de fertilizante-tiempo de siembra.
Paso 4: Calcular los grados de libertad (df):
Los grados de libertad definen el número de piezas de información independientes para cada efecto.
- glTotal: N-1 (observaciones totales menos 1)
- dfFertilizante: Número de tipos de fertilizantes -1
- dfTiempo de plantación: Número de veces de siembra -1
- dfInteracción: (Número de tipos de fertilizantes -1) * (Número de épocas de siembra -1)
- dfDentro de: dfTotal-dfFertilizador-dfplanting-dfInteracción
Paso 5: Calcular los cuadrados medios
Divide cada suma de cuadrados por su correspondiente grado de libertad.
- MS_Fertilizante: SSB_F/dfFertilizante
- MS_Tiempodeplantación: SSB_T/dfPlantación
- MS_Interacción: Interacción SSI/df
- MS_Dentro de: SSW/dfDentro
Paso 6: Calcular las estadísticas F
Calcule estadísticas F separadas para el tipo de fertilizante, el tiempo de siembra y el efecto de interacción:
- F_Fertilizar: MS_Fertilizante/MS_Dentro
- F_Tiempodeplantación: MS_PlantingTime/ MS_Dentro
- F_Interacción: MS_Inteacción/MS_Dentro
- F_Tiempodeplantación: MS_Tiempodeplantación/MS_Dentro
- F_Interacción: MS_Interacción/ MS_Dentro
Paso 7: Determinar los valores críticos y la decisión:
Elija un nivel de significancia (alfa) para su análisis, normalmente tomamos 0.05
Busque valores F críticos para cada efecto (fertilizante, tiempo de siembra, interacción) en el nivel alfa elegido y sus respectivos grados de libertad utilizando una tabla de distribución F o software estadístico.
Compare sus estadísticas F calculadas con los valores F críticos para cada efecto:
- Si el estadístico F es mayor que el valor F crítico, rechace la hipótesis nula (H0) para ese efecto. Esto indica una diferencia estadísticamente significativa.
- Si el estadístico F es menor o igual que el valor F crítico, no rechace H0 por ese efecto. Esto indica una diferencia estadísticamente insignificante.
Paso 8: Análisis post-hoc (si es necesario)
Si se rechaza la hipótesis nula, lo que significa una diferencia general significativa, es posible que desee profundizar más. Post-hoc como la diferencia honestamente significativa (HSD) de Tukey puede ayudar a identificar qué grupos de fertilizantes específicos tienen alturas promedio de plantas estadísticamente diferentes.
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols
# Create a DataFrame from the dictionary
plant_heights = {
'Treatment': ['A', 'A', 'A', 'A', 'A', 'A',
'B', 'B', 'B', 'B', 'B', 'B',
'C', 'C', 'C', 'C', 'C', 'C'],
'Time': ['Early', 'Early', 'Early', 'Late', 'Late', 'Late',
'Early', 'Early', 'Early', 'Late', 'Late', 'Late',
'Early', 'Early', 'Early', 'Late', 'Late', 'Late'],
'Height': [25, 28, 23, 27, 26, 24,
20, 22, 19, 21, 24, 22,
18, 20, 17, 19, 21, 20]
}
df = pd.DataFrame(plant_heights)
# Fit the ANOVA model
model = ols('Height ~ C(Treatment) + C(Time) + C(Treatment):C(Time)', data=df).fit()
# Perform ANOVA
anova_table = sm.stats.anova_lm(model, typ=2)
# Print the ANOVA table
print(anova_table)
# Interpret the results
alpha = 0.05 # Significance level
if anova_table['PR(>F)'][0] < alpha:
print("nReject null hypothesis for Treatment factor.")
else:
print("nFail to reject null hypothesis for Treatment factor.")
if anova_table['PR(>F)'][1] < alpha:
print("Reject null hypothesis for Time factor.")
else:
print("Fail to reject null hypothesis for Time factor.")
if anova_table['PR(>F)'][2] < alpha:
print("Reject null hypothesis for Interaction between Treatment and Time.")
else:
print("Fail to reject null hypothesis for Interaction between Treatment and Time.")
Salida:
Valor crítico F para el tratamiento en grado de libertad (2,12) con un nivel de significancia de 0.05 desde tabla de distribución F es 9.42
El valor F crítico para el tiempo en el grado de libertad (1,12) con un nivel de significancia de 0.05 es 61.22
F- el valor crítico para la interacción entre el tratamiento y el tiempo en un nivel de significancia de 0.05 en el grado de libertad (2,12) es 9.42
Dado que F-crítico < F-estadístico, rechazamos la hipótesis nula para el factor de tratamiento.
Pero para el factor tiempo y la interacción entre el tratamiento y el factor tiempo no pudimos rechazar la hipótesis nula como valor estadístico F > valor crítico F
Con un valor de p inferior a 0.05, nuestra conclusión sigue siendo consistente: rechazamos la hipótesis nula para el factor de tratamiento, mientras que con un valor de p superior a 0.05 no podemos rechazar la hipótesis nula para el factor tiempo y la interacción entre el factor tratamiento y el tiempo.
Diferencia entre ANOVA unidireccional y ANOVA bidireccional
El ANOVA unidireccional y el ANOVA bidireccional son técnicas estadísticas que se utilizan para analizar las diferencias entre grupos, pero difieren en términos del número de variables independientes que consideran y la complejidad del diseño experimental.
Estas son las diferencias clave entre ANOVA unidireccional y ANOVA bidireccional:
| Aspecto | ANOVA unidireccional | ANOVA bidireccional |
|---|---|---|
| Número de variables | Analiza una variable independiente (factor) en una variable dependiente continua | Analiza dos variables independientes (factores) en una variable dependiente continua. |
| Diseño Experimental | Una variable independiente categórica con múltiples niveles (grupos) | Dos variables categóricas independientes (factores), a menudo denominadas A y B, con múltiples niveles. Permite examinar los efectos principales y los efectos de interacción. |
| Interpretación | Indica diferencias significativas entre las medias del grupo. | Proporciona información sobre los principales efectos de los factores (A y B) y su interacción. Ayuda a evaluar las diferencias entre los niveles de factores y la interdependencia. |
| Complejidad | Relativamente sencillo y fácil de interpretar. | Más complejo, analizando los principales efectos de dos factores y su interacción. Requiere una cuidadosa consideración de las relaciones entre factores. |
Conclusión
ANOVA es una poderosa herramienta para analizar diferencias entre medias grupales, esencial cuando se comparan más de dos promedios muestrales. El ANOVA unidireccional evalúa el impacto de un solo factor en un resultado continuo, mientras que el ANOVA bidireccional extiende este análisis para considerar dos factores y sus efectos de interacción. Comprender estas diferencias permite a los investigadores elegir el enfoque analítico más adecuado para sus diseños experimentales y preguntas de investigación.
Preguntas frecuentes
R. ANOVA significa Análisis de Varianza, un método estadístico utilizado para analizar las diferencias entre las medias de los grupos. Se utiliza al comparar medias entre tres o más grupos para determinar si existen diferencias significativas.
R. El ANOVA unidireccional se utiliza cuando se tiene una variable independiente categórica (factor) con múltiples niveles y se desea comparar las medias de estos niveles. Por ejemplo, comparar la efectividad de diferentes tratamientos en un solo resultado.
R. El ANOVA de dos factores se utiliza cuando se tienen dos variables independientes categóricas (factores) y se desea analizar sus efectos sobre una variable dependiente continua, así como la interacción entre los dos factores. Es útil para estudiar los efectos combinados de dos factores en un resultado.
A. El valor p en ANOVA indica la probabilidad de observar los datos si la hipótesis nula (sin diferencia significativa entre las medias de los grupos) fuera cierta. Un valor p bajo (< 0.05) sugiere que existe evidencia significativa para rechazar la hipótesis nula y concluir que existen diferencias entre los grupos).
A. El estadístico F en ANOVA mide la relación entre la varianza entre grupos y la varianza dentro de los grupos. Una estadística F más alta indica que la varianza entre grupos es mayor en relación con la varianza dentro de los grupos, lo que sugiere una diferencia significativa entre las medias de los grupos.
- Distribución de relaciones públicas y contenido potenciado por SEO. Consiga amplificado hoy.
- PlatoData.Network Vertical Generativo Ai. Empodérate. Accede Aquí.
- PlatoAiStream. Inteligencia Web3. Conocimiento amplificado. Accede Aquí.
- PlatoESG. Carbón, tecnología limpia, Energía, Ambiente, Solar, Gestión de residuos. Accede Aquí.
- PlatoSalud. Inteligencia en Biotecnología y Ensayos Clínicos. Accede Aquí.
- Fuente: https://www.analyticsvidhya.com/blog/2024/04/one-way-and-two-way-analysis-of-variance-anova/



