Vitalik Buterin a través de Blog de Vitalik Buterin

Este es un espejo de la publicación en https://medium.com/@VitalikButerin/explorando-parejos-de-curvas-elípticas-c73c1864e627

Advertencia de activación: matemáticas.

Una de las primitivas criptográficas clave detrás de varias construcciones, incluidas las firmas de umbral deterministas, zk-SNARK y otras formas más simples de pruebas de conocimiento cero, es el emparejamiento de curvas elípticas. Los pares de curvas elípticas (o “mapas bilineales”) son una adición reciente a una historia de 30 años de uso de curvas elípticas para aplicaciones criptográficas, incluido el cifrado y las firmas digitales; los emparejamientos introducen una forma de "multiplicación cifrada", ampliando enormemente lo que pueden hacer los protocolos basados ​​en curvas elípticas. El propósito de este artículo será profundizar en los pares de curvas elípticas y explicar un esquema general de cómo funcionan.

No se espera que usted entienda todo lo que contiene la primera vez que lo lea, ni siquiera la décima vez; Esto es realmente difícil. Pero esperamos que este artículo le dé al menos una idea de lo que sucede bajo el capó.

Las curvas elípticas en sí mismas son un tema nada trivial de entender y este artículo generalmente asumirá que usted sabe cómo funcionan; Si no es así, le recomiendo este artículo como introducción: https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/. Como resumen rápido, la criptografía de curva elíptica involucra objetos matemáticos llamados "puntos" (estos son puntos bidimensionales literales con coordenadas (�,�)), con fórmulas especiales para sumarlos y restarlos (es decir, para calcular las coordenadas de �= �+�), y también puedes multiplicar un punto por un número entero (es decir, �⋅�=�+�+…+�, aunque hay una forma mucho más rápida de calcularlo si � es grande).

Así es como se ve gráficamente la suma de puntos.

Existe un punto especial llamado “punto en el infinito” (�), el equivalente al cero en aritmética puntual; siempre es el caso que �+�=�. Además, una curva tiene un “solicite“; existe un número � tal que �⋅�=� para cualquier � (y por supuesto, �⋅(�+1)=�,�⋅(7⋅�+5)=�⋅5, y así sucesivamente). También existe un “punto generador” comúnmente acordado, �, que se entiende que en cierto sentido representa el número 1. Teóricamente, cualquier punto en una curva (excepto �) puede ser �; lo único que importa es que esté estandarizado.

Los emparejamientos van un paso más allá al permitirle verificar ciertos tipos de ecuaciones más complicadas en puntos de curvas elípticas; por ejemplo, si �=�⋅�,�=�⋅� y �=�⋅�, puede verificar si o no �⋅�=�, teniendo solo �,� y � como entradas. Esto podría parecer como si se estuvieran rompiendo las garantías de seguridad fundamentales de las curvas elípticas, ya que se filtra información sobre � simplemente conociendo P, pero resulta que la fuga está muy contenida; específicamente, la problema decisional de Diffie Hellman es fácil, pero el problema computacional de Diffie Hellman (conociendo � y � en el ejemplo anterior, informática �=�⋅�⋅�) y el problema de logaritmo discreto (recuperar � de �) siguen siendo computacionalmente inviables (al menos, si lo fueran antes).

Una tercera forma de ver lo que hacen los emparejamientos, y una que quizás sea más esclarecedora para la mayoría de los casos de uso que estamos tratando, es que si se ven los puntos de la curva elíptica como números cifrados unidireccionales (es decir, ���� ���(�)=�⋅�=�), entonces, mientras que las matemáticas tradicionales de curvas elípticas te permiten comprobar lineal restricciones en los números (por ejemplo, si �=�⋅�,�=�⋅� y �=�⋅�, verificar 5⋅�+7⋅�=11⋅� es realmente comprobando que 5⋅�+7⋅�=11⋅�), los emparejamientos te permiten comprobar cuadrático restricciones (por ejemplo, comprobar que �(�,�)⋅�(�,�⋅5)=1 es realmente comprobando que �⋅�+5=0). Y subir a cuadrática es suficiente para permitirnos trabajar con firmas de umbral deterministas, programas de aritmética cuadrática y todas esas otras cosas buenas.

Ahora bien, ¿qué es este divertido operador �(�,�) que presentamos anteriormente? Este es el binomio. Los matemáticos a veces también lo llaman mapa bilineal; la palabra "bilineal" aquí básicamente significa que satisface las restricciones:

�(�,�+�)=�(�,�)⋅�(�,�)

�(�+�,�)=�(�,�)⋅�(�,�)

Tenga en cuenta que + y ⋅ pueden ser operadores arbitrarios; Cuando creas nuevos y elegantes tipos de objetos matemáticos, al álgebra abstracta no le importa cómo son + y ⋅. se define, siempre y cuando sean consistentes en las formas habituales, por ejemplo. �+�=�+�,(�⋅�)⋅�=�⋅(�⋅�) y (�⋅�)+(�⋅�)=(�+�)⋅�.

Si �, �, � y � fueran simples números, entonces hacer un emparejamiento simple es fácil: podemos hacer �(�,�)=2��. Entonces, podemos ver:

�(3,4+5)=23⋅9=227

�(3,4)⋅�(3,5)=23⋅4⋅23⋅5=212⋅215=227

¡Es bilineal!

Sin embargo, estos pares simples no son adecuados para la criptografía porque los objetos con los que trabajan son números enteros simples y demasiado fáciles de analizar; los números enteros facilitan la división, el cálculo de logaritmos y otros cálculos diversos; Los números enteros simples no tienen el concepto de "clave pública" o "función unidireccional". Además, con el emparejamiento descrito anteriormente puedes retroceder: sabiendo �, y sabiendo �(�,�), puedes simplemente calcular una división y un logaritmo para determinar �. Queremos objetos matemáticos que se acerquen lo más posible a “cajas negras”, donde se puedan sumar, restar, multiplicar y dividir. pero no hagas nada más. Aquí es donde entran en juego las curvas elípticas y los pares de curvas elípticas.

Resulta que es posible hacer un mapa bilineal sobre puntos de curva elíptica, es decir, generar una función �(�,�) donde las entradas � y � sean puntos de curva elíptica, y donde la salida sea lo que se llama una (��)12 elemento (al menos en el caso específico que cubriremos aquí; los detalles difieren dependiendo de los detalles de la curva, más sobre esto más adelante), pero las matemáticas detrás de hacerlo son bastante complejas.

Primero, cubramos los campos primos y los campos de extensión. La curva bastante elíptica en la imagen anterior en esta publicación solo se ve así si se supone que la ecuación de la curva se define usando números reales regulares. Sin embargo, si realmente usamos números reales regulares en criptografía, entonces puedes usar logaritmos para "retroceder" y todo se rompe; Además, la cantidad de espacio necesario para almacenar y representar los números puede crecer arbitrariamente. Por lo tanto, en lugar de eso usamos números en un primer campo.

Un campo primo consta del conjunto de números 0,1,2…�−1, donde � es primo, y las distintas operaciones se definen de la siguiente manera:

�+�:(�+�) % �

�⋅�:(�⋅�) % �

�−�:(�−�) % �

�/�:(�⋅��−2) % �

Básicamente, todas las matemáticas se hacen módulo � (ver esta página para una introducción a las matemáticas modulares). La división es un caso especial; normalmente, 32 no es un número entero, y aquí queremos tratar solo con números enteros, por lo que intentamos encontrar el número � tal que �⋅2=3, donde ⋅, por supuesto, se refiere a la multiplicación modular como se definió anteriormente. Gracias a El pequeño teorema de Fermat, el truco de exponenciación que se muestra arriba funciona, pero también hay una manera más rápida de hacerlo, usando el Algoritmo euclidiano extendido. Supongamos �=7; Aquí están algunos ejemplos:

2+3=5 % 7=5

4+6=10 % 7=3

2−5=−3 % 7=4

6⋅3=18 % 7=4

3/2=(3⋅25) % 7=5

5⋅2=10 % 7=3

Si juegas con este tipo de matemáticas, notarás que es perfectamente consistente y satisface todas las reglas habituales. Los dos últimos ejemplos anteriores muestran cómo (�/�)⋅�=�; También puedes ver que (�+�)+�=�+(�+�),(�+�)⋅�=�⋅�+�⋅�, y todas las demás identidades algebraicas de la escuela secundaria que conoces y amas continúan para ser cierto también. En realidad, en las curvas elípticas, los puntos y las ecuaciones suelen calcularse en campos primos.

Ahora, hablemos de campos de extensión. Probablemente ya hayas visto un campo de extensión antes; El ejemplo más común que encontramos en los libros de texto de matemáticas es el campo de los números complejos, donde el campo de los números reales se “extiende” con el elemento adicional −1=�. Básicamente, los campos de extensión funcionan tomando un campo existente, luego “inventando” un nuevo elemento y definiendo la relación entre ese elemento y los elementos existentes (en este caso, �2+1=0), asegurándose de que esta ecuación no sea cierta. para cualquier número que esté en el campo original, y mirando el conjunto de todas las combinaciones lineales de elementos del campo original y el nuevo elemento que acabas de crear.

También podemos hacer extensiones de campos primos; por ejemplo, podemos extender el campo primo mod7 que describimos anteriormente con �, y luego podemos hacer:

(2+3�)+(4+2�)=6+5�

(5+2�)+3=1+2�

(6+2�)⋅2=5+4�

4�⋅(2+�)=3+�

Ese último resultado puede ser un poco difícil de entender; Lo que pasó allí fue que primero descompusimos el producto en 4�⋅2+4�⋅�, lo que da 8�−4, y luego, como estamos trabajando en matemáticas mod7, se convierte en �+3. Para dividir hacemos:

�/�:(�⋅�(�2−2)) % �

Tenga en cuenta que el exponente del pequeño teorema de Fermat ahora es �2 en lugar de �, aunque una vez más, si queremos ser más eficientes, también podemos extender el algoritmo euclidiano extendido para hacer el trabajo. Tenga en cuenta que ��2−1=1 para cualquier � en este campo, por lo que llamamos �2−1 el “orden del grupo multiplicativo en el campo”.

Con números reales, el Teorema fundamental del álgebra garantiza que la extensión cuadrática que llamamos números complejos sea “completa”; no se puede extender más, porque para cualquier relación matemática (al menos, cualquier relación matemática definida por una fórmula algebraica) que se pueda encontrar entre algún elemento nuevo � y los números complejos existentes, es posible encontrar al menos un número complejo que ya satisfaga esa relación. Sin embargo, con los campos primos no tenemos este problema, por lo que podemos ir más allá y hacer extensiones cúbicas (donde la relación matemática entre algún elemento nuevo � y los elementos del campo existentes es una ecuación cúbica, por lo que 1,� y �2 son todos linealmente independientes entre sí), extensiones de orden superior, extensiones de extensiones, etc. Y son estos tipos de números complejos modulares sobrealimentados sobre los que se construyen los pares de curvas elípticas.

Para aquellos interesados ​​en ver las matemáticas exactas involucradas en la realización de todas estas operaciones escritas en código, aquí se implementan campos principales y extensiones de campo: https://github.com/ethereum/py_pairing/blob/master/py_ecc/bn128/bn128_field_elements.py

Ahora, pasemos a los pares de curvas elípticas. Un emparejamiento de curvas elípticas (o más bien, la forma específica de emparejamiento que exploraremos aquí; también hay otros tipos de emparejamientos, aunque su lógica es bastante similar) es un mapa �2×�1→��, donde:

• �1 es una curva elíptica, donde los puntos satisfacen una ecuación de la forma �2=�3+�, y donde ambas coordenadas son elementos de �� (es decir, son números simples, excepto que la aritmética se hace en módulo de algún número primo)
• �2 es una curva elíptica, donde los puntos satisfacen la misma ecuación que �1, excepto donde las coordenadas son elementos de (��)12 (es decir, son los números complejos sobrealimentados de los que hablamos anteriormente; definimos un nuevo “número mágico” ” �, que está definido por un polinomio de grado 12 como �12−18⋅�6+82=0)
• �� es el tipo de objeto al que va el resultado de la curva elíptica. En las curvas que observamos, �� es (��)12 (el mismo número complejo sobrealimentado que se usa en �2)

La principal propiedad que debe satisfacer es la bilinealidad, que en este contexto significa que:

• �(�,�+�)=�(�,�)⋅�(�,�)
• �(�+�,�)=�(�,�)⋅�(�,�)

Hay otros dos criterios importantes:

• Computabilidad eficiente (por ejemplo, podemos hacer un emparejamiento fácil simplemente tomando los logaritmos discretos de todos los puntos y multiplicándolos, pero esto es tan difícil desde el punto de vista computacional como romper la criptografía de curva elíptica en primer lugar, por lo que no cuenta)
• No degeneración (claro, podrías definir simplemente �(�,�)=1, pero esa no es una combinación particularmente útil)

¿Entonces como hacemos esto?

Las matemáticas detrás de por qué funcionan las funciones de emparejamiento son bastante complicadas e implican bastante álgebra avanzada que va incluso más allá de lo que hemos visto hasta ahora, pero proporcionaré un resumen. En primer lugar, debemos definir el concepto de divisor, básicamente una forma alternativa de representar funciones en puntos de curvas elípticas. Un divisor de una función básicamente cuenta los ceros y los infinitos de la función. Para ver lo que esto significa, veamos algunos ejemplos. Fijemos algún punto �=(��,��), y consideremos la siguiente función:

�(�,�)=�−��

El divisor es [�]+[−�]−2⋅[�] (los corchetes se usan para representar el hecho de que nos estamos refiriendo a la presencia del punto � en el conjunto de ceros e infinitos de la función, no el punto P en sí; [�]+[�] es no lo mismo que [�+�]). El razonamiento es como sigue:

• La función es igual a cero en �, ya que � is ��, entonces �−��=0
• La función es igual a cero en −�, ya que −� y � comparten la misma coordenada �
• La función va al infinito cuando � va al infinito, por lo que decimos que la función es igual al infinito en �. Hay una razón técnica por la que este infinito necesita contarse dos veces, por lo que � se suma con una “multiplicidad” de −2 (negativa porque es un infinito y no un cero, dos debido a este doble conteo).

La razón técnica es más o menos la siguiente: debido a que la ecuación de la curva es �3=�2+�,� va al infinito “1.5 veces más rápido” que � para que �2 pueda seguir el ritmo de �3; por lo tanto, si una función lineal incluye solo � entonces se representa como una infinidad de multiplicidad 2, pero si incluye � entonces se representa como una infinidad de multiplicidad 3.

Ahora, considere una “función de línea”:

��+��+�=0

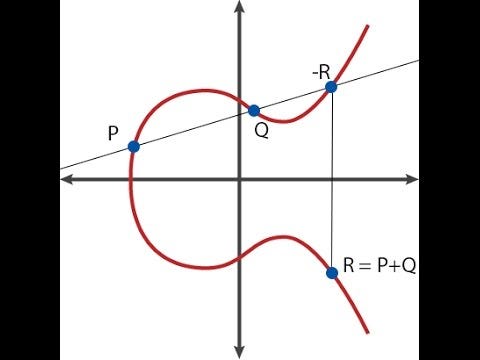
Donde �, � y � se eligen cuidadosamente para que la línea pase por los puntos � y �. Debido a cómo funciona la suma de curvas elípticas (consulte el diagrama en la parte superior), esto también significa que pasa por −�−�. Y llega hasta el infinito dependiendo tanto de � como de �, por lo que el divisor se convierte en [�]+[�]+[−�−�]−3⋅[�].

Sabemos que cada “función racional” (es decir, una función definida sólo usando un número finito de operaciones +,−,⋅ y / en las coordenadas del punto) corresponde únicamente a algún divisor, hasta la multiplicación por una constante (es decir. si dos funciones � y � tienen el mismo divisor, entonces �=�⋅� para alguna constante �).

Para dos funciones cualesquiera � y �, el divisor de �⋅� es igual al divisor de � más el divisor de � (en los libros de texto de matemáticas, verás (�⋅�)=(�)+(�)), así, por ejemplo, si �(�,�)=��−�, entonces (�3)=3⋅[�]+3⋅[−�]−6⋅[�]; � y −� se “cuentan tres veces” para tener en cuenta el hecho de que �3 tiende a 0 en esos puntos “tres veces más rápido” en cierto sentido matemático.

Tenga en cuenta que hay un teorema que establece que si “quita los corchetes” de un divisor de una función, los puntos deben sumar �([�]+[�]+[−�−�]−3⋅[ �] encaja claramente, ya que �+�−�−�−3⋅�=�), y cualquier divisor que tenga esta propiedad es el divisor de una función.

Ahora estamos listos para ver las parejas de Tate. Considere las siguientes funciones, definidas mediante sus divisores:

• (��)=�⋅[�]−�⋅[�], donde � es el orden de �1, es decir. �⋅�=� para cualquier �
• (��)=�⋅[�]−�⋅[�]
• (�)=[�+�]−[�]−[�]+[�]

Ahora, veamos el producto ��⋅��⋅��. El divisor es:

�⋅[�]−�⋅[�]+�⋅[�]−�⋅[�]+�⋅[�+�]−�⋅[�]−�⋅[�]+�⋅[�]

Lo que se simplifica claramente a:

�⋅[�+�]−�⋅[�]

Observe que este divisor tiene exactamente el mismo formato que el divisor de �� y �� anterior. Por lo tanto, ��⋅��⋅��=��+�.

Ahora, introducimos un procedimiento llamado paso de “exponenciación final”, donde tomamos el resultado de nuestras funciones anteriores (��,��, etc.) y lo elevamos a la potencia �=(�12−1)/�, donde �12−1 es el orden del grupo multiplicativo en (��)12 (es decir, para cualquier �∈(��)12,�(�12−1)=1). Observe que si aplica esta exponenciación a cualquier resultado que tenga ya haya utilizado elevado a la potencia de �, se obtiene una exponenciación a la potencia de �12−1, por lo que el resultado se convierte en 1. Por lo tanto, después de la exponenciación final, �� se cancela y obtenemos ���⋅���=( ��+�)�. Hay algo de bilinealidad para ti.

Ahora, si quieres crear una función que sea bilineal en ambos argumentos, necesitas recurrir a matemáticas más espeluznantes, donde en lugar de tomar �� de un valor directamente, tomas �� de un divisor, y de ahí proviene el “maridaje Tate” completo. Para demostrar más resultados hay que lidiar con nociones como “equivalencia lineal” y “reciprocidad de Weil”, y la madriguera del conejo continúa a partir de ahí. Puedes encontrar más material de lectura sobre todo esto. esta página y esta página.

Para una implementación de una versión modificada del emparejamiento de Tate, llamado emparejamiento óptimo de Ate, mire aquí. El código implementa algoritmo de miller, que es necesario para calcular realmente ��.

Tenga en cuenta que el hecho de que emparejamientos como este sean posibles es una bendición a medias: por un lado, significa que todos los protocolos que podemos hacer con los emparejamientos se vuelven posibles, pero también significa que debemos tener más cuidado con las curvas elípticas. usamos.

Cada curva elíptica tiene un valor llamado grado de incrustación; esencialmente, el � más pequeño tal que ��−1 es un múltiplo de � (donde � es el número primo utilizado para el campo y � es el orden de la curva). En los campos anteriores, �=12, y en los campos utilizados para ECC tradicional (es decir, donde no nos importan los emparejamientos), el grado de incrustación es a menudo extremadamente grande, hasta el punto de que los emparejamientos son computacionalmente inviables; sin embargo, si no tenemos cuidado entonces podemos generar campos donde �=4 o incluso 1.

Si �=1, entonces el problema del “logaritmo discreto” para curvas elípticas (esencialmente, recuperar � conociendo sólo el punto �=�⋅�, el problema que hay que resolver para “descifrar” una clave privada de curva elíptica) se puede reducir en un problema matemático similar sobre ��, donde el problema se vuelve mucho más fácil (esto se llama ataque MOV); El uso de curvas con un grado de incrustación de 12 o superior garantiza que esta reducción no esté disponible o que resolver el problema del registro discreto sobre los resultados del emparejamiento sea al menos tan difícil como recuperar una clave privada a partir de una clave pública "de la manera normal" (es decir, computacionalmente inviable). No te preocupes; Todos los parámetros de la curva estándar se han verificado minuciosamente para detectar este problema.

Estén atentos para una explicación matemática de cómo funcionan los zk-SNARK, próximamente.

Un agradecimiento especial a Christian Reitwiessner, Ariel Gabizon (de Zcash) y Alfred Menezes por revisar y hacer correcciones.

• Distribución de relaciones públicas y contenido potenciado por SEO. Consiga amplificado hoy.
• PlatoData.Network Vertical Generativo Ai. Empodérate. Accede Aquí.
• PlatoAiStream. Inteligencia Web3. Conocimiento amplificado. Accede Aquí.
• PlatoESG. Carbón, tecnología limpia, Energía, Ambiente, Solar, Gestión de residuos. Accede Aquí.
• PlatoSalud. Inteligencia en Biotecnología y Ensayos Clínicos. Accede Aquí.
• Desplazamientos de bloque. Modernización de la propiedad de compensaciones ambientales. Accede Aquí.
• Fuente: Inteligencia de datos de Platón.