Introducción
En este artículo exploraremos qué es evaluación de la hipótesis, enfocándonos en la formulación de hipótesis nulas y alternativas, estableciendo pruebas de hipótesis y profundizaremos en las pruebas paramétricas y no paramétricas, discutiendo sus respectivos supuestos e implementación en Python. Pero nos centraremos principalmente en pruebas no paramétricas como la prueba U de Mann-Whitney y la prueba de Kruskal-Wallis. Al final, tendrá una comprensión integral de las pruebas de hipótesis y las herramientas prácticas para aplicar estos conceptos en sus propios análisis estadísticos.
OBJETIVOS DE APRENDIZAJE
- Comprender los principios de la prueba de hipótesis, incluida la formulación de hipótesis nulas y alternativas.
- Configuración de la prueba de hipótesis.
- Comprensión de las Pruebas Paramétricas y sus tipos.
- Comprensión de las pruebas no paramétricas y sus tipos junto con sus implementaciones.
- Diferencia entre Paramétrico y No Paramétrico.
Tabla de contenidos.
¿Qué es la prueba de hipótesis?
Una hipótesis es una afirmación hecha por una persona/organización. La afirmación suele ser sobre parámetros poblacionales como la media o la proporción y buscamos evidencia de una muestra para respaldar la afirmación.
La prueba de hipótesis, a veces denominada prueba de significancia, es un método para confirmar una afirmación o hipótesis sobre un parámetro en una población utilizando datos medidos en una muestra. Usando este método, exploramos varias teorías determinando la potencialidad de que, si la hipótesis del parámetro poblacional hubiera sido cierta, se podría haber seleccionado una estadística de muestra.
La prueba de hipótesis implica la formulación de dos hipótesis:
- Hipótesis nula (H0)
- Hipótesis alternativa (H1)
Hipótesis nula : Generalmente es una hipótesis de no diferencia y generalmente se denota por H0. Según RA Fisher, la hipótesis nula es la hipótesis que se prueba para detectar un posible rechazo bajo el supuesto de que es cierta (Ref. Fundamentos de estadística matemática).
Hipótesis alternativa: Cualquier hipótesis que sea complementaria a la hipótesis nula se denomina hipótesis alternativa, normalmente denotada por H1.
El objetivo de la prueba de hipótesis es rechazar o mantener una hipótesis nula para establecer una relación estadísticamente significativa entre dos variables (normalmente una independiente y otra dependiente, es decir, normalmente una es la causa y la otra es el efecto).
Configuración de la prueba de hipótesis
- Describe la hipótesis con palabras o haz una afirmación.
- Con base en la afirmación se definen hipótesis nulas y alternativas.
- Identifique el tipo de prueba de hipótesis apropiada para la afirmación anterior.
- Identifique las estadísticas de prueba que se utilizarán para probar la validez de la hipótesis nula.
- Decidir los criterios de rechazo y retención de la hipótesis nula. A esto se le llama valor de significancia, tradicionalmente denotado con el símbolo α (alfa).
- Calcule el valor p, que es la probabilidad condicional de observar el valor del estadístico de prueba cuando la hipótesis nula es verdadera. En términos simples, el valor p es la evidencia que respalda la hipótesis nula.
Prueba paramétrica y no paramétrica
Las pruebas estadísticas no paramétricas no se basan en suposiciones sobre los parámetros de las distribuciones poblacionales de las que se muestrean los datos, mientras que las pruebas estadísticas paramétricas sí lo hacen.
Pruebas paramétricas
La mayoría de las pruebas estadísticas se realizan utilizando un conjunto de supuestos como base. El análisis puede arrojar conclusiones engañosas o completamente falsas cuando se violan ciertos supuestos.
Normalmente los supuestos son:
- Normalidad: la distribución muestral de los parámetros a probar sigue una distribución normal (o al menos simétrica).
- Homogeneidad de las varianzas: la varianza de los datos es la misma en diferentes grupos, a menos que estemos probando medias poblacionales provenientes de dos poblaciones diferentes.
Algunas de las pruebas paramétricas son:
- Prueba Z: Pruebe la media, la varianza o la proporción de la población cuando se conoce la desviación estándar de la población.
- Prueba t de Student: Pruebe la media, la varianza o la proporción de la población cuando no se conoce la desviación estándar de la población.
- Prueba t pareada: Se utiliza para comparar las medias de dos grupos o condiciones relacionados.
- Análisis de Varianza (ANOVA): Se utiliza para comparar medias entre tres o más grupos independientes.
- Análisis de regresión: Se utiliza para evaluar la relación entre una o más variables independientes y una variable dependiente.
- Análisis de Covarianza (ANCOVA): Extiende ANOVA incorporando covariables adicionales en el análisis.
- Análisis Multivariado de Varianza (MANOVA): Extiende ANOVA para evaluar diferencias en múltiples variables dependientes entre grupos.
Ahora profundicemos en las pruebas no paramétricas.
Prueba no paramétrica
Por primera vez, Wolfowitz utilizó el término "no paramétrica" en 1942. Para comprender la idea de estadística no paramétrica, primero se debe tener una comprensión básica de la estadística paramétrica, que acabamos de analizar. A prueba paramétrica Requiere una muestra que sigue una distribución específica (generalmente normal). Además, las pruebas no paramétricas son independientes de supuestos paramétricos como la normalidad.
Pruebas no paramétricas (también conocidas como pruebas libres de distribución ya que no tienen supuestos sobre la distribución de la población). Las pruebas no paramétricas implican que las pruebas no se basan en el supuesto de que los datos se extraen de una Distribución de probabilidad definido a través de parámetros como media, proporción y desviación estándar.
Las pruebas no paramétricas se utilizan cuando:
- La prueba no se trata de parámetros poblacionales como la media o la proporción.
- El método no requiere suposiciones sobre la distribución de la población (como que la población sigue una distribución normal).
Tipos de pruebas no paramétricas
Ahora analicemos el concepto y el procedimiento para realizar la prueba de Chi-cuadrado, la prueba de Mann-Whitney, la prueba de rango con signo de Wilcoxon y las pruebas de Kruskal-Wallis:
Prueba de chi-cuadrado
Para determinar si la asociación entre dos variables cualitativas es estadísticamente significativa, se debe realizar una prueba de significancia llamada Prueba de Chi-Cuadrado.
Hay dos tipos principales de pruebas de Chi-Cuadrado:
Bondad de ajuste de Chi cuadrado
Utilice la prueba de bondad de ajuste para decidir si una población con una distribución desconocida "se ajusta" a una distribución conocida. En este caso habrá una única pregunta de encuesta cualitativa o un único resultado de un experimento de una única población. La bondad de ajuste se utiliza normalmente para ver si la población es uniforme (todos los resultados ocurren con la misma frecuencia), la población es normal o la población es la misma que otra población con una distribución conocida. Las hipótesis nula y alternativa son:
- H0: La población se ajusta a la distribución dada.
- Ha: La población no se ajusta a la distribución dada.
Entendamos esto con un ejemplo
| Día | Lunes | Martes | Miércoles | jueves | Viernes | Sábado | Domingo |
| Número de averías | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
La tabla muestra el número de averías de un factor. En este ejemplo, solo hay una variable y tenemos que determinar si la distribución observada (dada en la tabla) se ajusta a la distribución esperada o no.
Para esto la hipótesis nula y la hipótesis alternativa se formularán como:
- H0:Las averías se distribuyen uniformemente.
- Ha: Los desgloses no están distribuidos uniformemente.
Y el grado de libertad será n-1 (en este caso n=7, entonces df = 7-1=6)
Expected value will be= (14+22+16+18+12+19+11)/7=16
| Día | Lunes | Martes | Miércoles | jueves | Viernes | Sábado | Domingo |
| Número de averías (observadas) | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
| esperado | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| (observado-esperado) | -2 | 6 | 0 | 2 | -4 | 3 | -5 |
| (observado-esperado)^2 | 4 | 36 | 0 | 4 | 16 | 9 | 25 |
Usando esta fórmula Calcular Chi-cuadrado
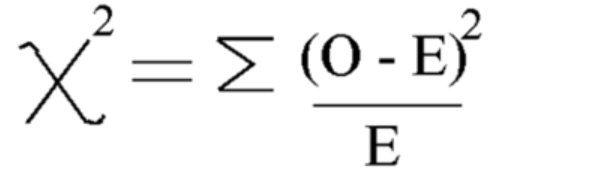
Chi-cuadrado = 5.875
Y el grado de libertad es = n-1=7-1=6
Ahora veamos el valor crítico de tabla de distribución de chi cuadrado al 5 % de nivel de significancia
Entonces el valor crítico es 12.592
Dado que el valor calculado de Chi-cuadrado es menor que el valor crítico, aceptamos la hipótesis nula y podemos concluir que los desgloses están distribuidos uniformemente.
Prueba de independencia de chi-cuadrado
Utilice la prueba de independencia para decidir si dos variables (factores) son independientes o dependientes, es decir, si estas dos variables tienen una relación de asociación significativa entre ellas o no. En este caso se realizarán dos preguntas de encuesta o experimentos cualitativos y se construirá una tabla de contingencia. El objetivo es ver si las dos variables no están relacionadas (independientes) o están relacionadas (dependientes). Las hipótesis nula y alternativa son:
- H0: Las dos variables (factores) son independientes.
- Ha: Las dos variables (factores) son dependientes.
Tomemos un ejemplo
Ejemplo en el que queremos investigar si el género y el color preferido de camisa eran independientes. Esto significa que queremos saber si el género de una persona influye en su elección de color. Realizamos una encuesta y organizamos los datos en la tabla.
En esta tabla se observan los valores:
| Negro | Blanco | Rojo | Azul | |
| Masculino | 48 | 12 | 33 | 57 |
| Femenino | 34 | 46 | 42 | 26 |
Ahora primero formule hipótesis nulas y alternativas.
- H0: El género y el color de camisa preferido son independientes.
- Ha: El género y el color de camisa preferido no son independientes
Para calcular las estadísticas de la prueba de Chi-cuadrado necesitamos calcular el valor esperado. Entonces, suma todas las filas y columnas y los totales generales:
| Negro | Blanco | Rojo | Azul | Total | |
| Masculino | 48 | 12 | 33 | 57 | 150 |
| Femenino | 34 | 46 | 42 | 26 | 148 |
| Total | 82 | 58 | 75 | 83 | 298 |
Después de esto, podemos calcular la tabla de valores esperados de la tabla anterior para cada entrada usando esta fórmula = (total de fila * total de columna)/total general
Tabla de valores esperados:
| Negro | Blanco | Rojo | Azul | |
| Masculino | 41.3 | 29.2 | 37.8 | 41.8 |
| Femenino | 40.7 | 28.8 | 37.2 | 41.2 |
Ahora calcule el valor de Chi cuadrado usando la fórmula para la prueba de chi-cuadrado:
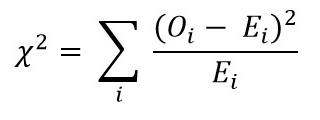
- Oi = Valor observado
- Ei = valor esperado
El valor que obtenemos es: Χ2 = 34.9572
Calcular el grado de libertad
DF=(número de fila-1)*(número de columna-1)
Ahora encuentre y compare el valor crítico con la prueba de chi-cuadrado. valor estadístico:
Para hacer esto, puede buscar el grado de libertad y el nivel de significancia (alfa) de la tabla de distribución de chi-cuadrado
En alfa = 0.050, obtendremos un valor crítico = 7.815
Desde chi-cuadrado> valor crítico
Por tanto, rechazamos la hipótesis nula y podemos concluir que el género y el color de camisa preferido no son independientes.
Implementación de Chi-Cuadrado
Ahora, veamos la implementación de Chi-Square usando algún ejemplo de la vida real en Python:
- H0: El género y el color de camisa preferido son independientes.
- Ha: El género y el color de camisa preferido no son independientes
Creando conjunto de datos:
import pandas as pd
from scipy.stats import chi2_contingency
from scipy.stats import chi2
# Given dataset
df_dict = {
'Black': [48, 34],
'White': [12, 46],
'Red': [33, 42],
'Blue': [57, 26]
}
dataset_table = pd.DataFrame(df_dict, index=['Male', 'Female'])
print("Dataset Table:")
print(dataset_table)
print()
# Observed Values
Observed_Values = dataset_table.values
print("Observed Values:")
print(Observed_Values)
print()
# Perform chi-square test
val = chi2_contingency(dataset_table)
Expected_Values = val[3]
print("Expected Values:")
print(Expected_Values)
print()
# Degree of Freedom
no_of_rows = len(dataset_table.iloc[0:2, 0])
no_of_columns = 4
ddof = (no_of_rows - 1) * (no_of_columns - 1)
print("Degree of Freedom:", ddof)
print()
# Chi-square statistic
chi_square = sum([(o - e) ** 2. / e for o, e in zip(Observed_Values, Expected_Values)])
chi_square_statistic = chi_square[0] + chi_square[1]
print("Chi-square statistic:", chi_square_statistic)
print()
# Critical value
alpha = 0.05
critical_value = chi2.ppf(q=1-alpha, df=ddof)
print('Critical value:', critical_value)
print()
# p-value
p_value = 1 - chi2.cdf(x=chi_square_statistic, df=ddof)
print('p-value:', p_value)
print()
# Significance level
print('Significance level:', alpha)
print('p-value:', p_value)
print('Degree of Freedom:', ddof)
print()
# Hypothesis testing
if chi_square_statistic >= critical_value:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
print()
if p_value <= alpha:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
Salida:
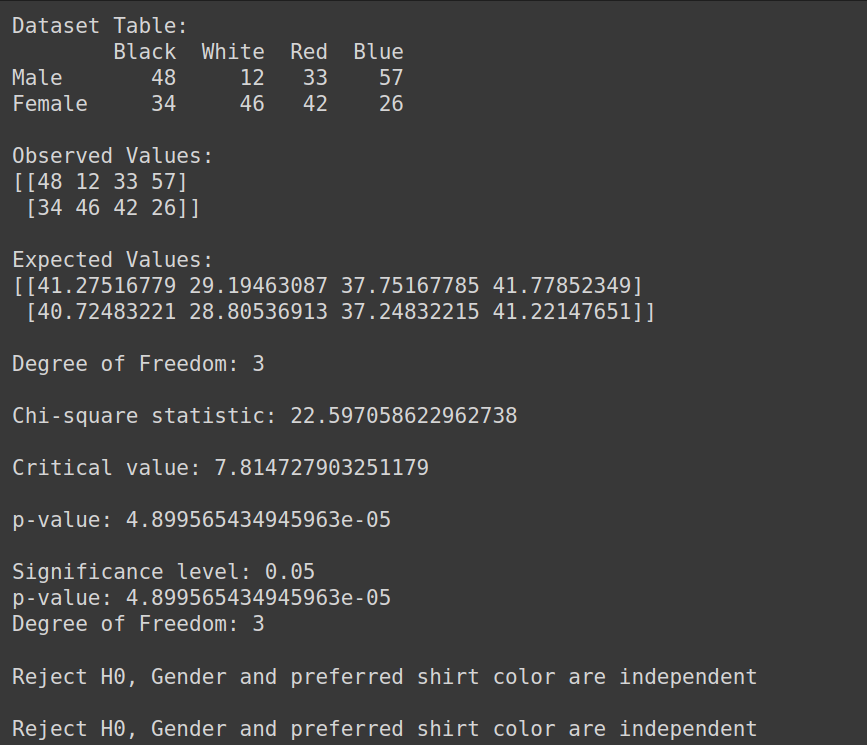
Prueba U de Mann-Whitney
La prueba U de Mann-Whitney sirve como alternativa no paramétrica a la prueba t para muestras independientes. Compara dos medias muestrales de la misma población, determinando si son iguales. Esta prueba se utiliza normalmente para datos ordinales o cuando no se cumplen los supuestos de la prueba t.
La prueba U de Mann-Whitney clasifica todos los valores de ambos grupos juntos y luego suma las clasificaciones de cada grupo. Calcula el estadístico de prueba, U, basándose en estos rangos. El estadístico U se compara con un valor crítico de una tabla o se calcula mediante una aproximación. Si el estadístico U es menor que el valor crítico, se rechaza la hipótesis nula.
Esto es diferente de las pruebas paramétricas como la prueba t, que comparan medias y asumen una distribución normal. En cambio, la prueba U de Mann-Whitney compara rangos y no requiere asumir una distribución normal.
Comprender la prueba U de Mann-Whitney puede resultar difícil porque los resultados se presentan en diferencias de rango de grupo en lugar de diferencias de medias de grupo.
Fórmula para la prueba de Mann-Whitney:
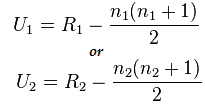
U= mín(U1,U2)
Aquí,
- U= Prueba U de Mann-Whitney
- n1= tamaño de muestra uno
- n2= tamaño de muestra dos
- R1= Rango del tamaño de muestra uno
- R2= Rango del tamaño de muestra 2
Entonces, entendamos esto con un breve ejemplo:
Supongamos que queremos comparar la eficacia de dos métodos de tratamiento diferentes (Método A y Método B) para mejorar la salud de los pacientes. Tenemos los siguientes datos:
- Método A: 3,4,2,6,2,5
- Método B: 9,7,5,10,6,8
Aquí podemos ver que los datos no se distribuyen normalmente y los tamaños de muestra son pequeños.
Implementación de la prueba U de Mann-Whitney
Ahora, realicemos la prueba U de Mann-Whitney:
Pero primero formulemos la hipótesis nula y alternativa.
- H0: No hay diferencia entre el Rank de cada tratamiento
- Ha: Hay una diferencia entre el Rank de cada tratamiento
Combina todos los tratamientos: 3,4,2,6,2,5,9,7,5,10,6,8
Datos ordenados: 2,2,3,4,5,5,6,6,7,8,9,10
Rango de datos ordenados: 1,2,3,4,5,6,7,8,9,10,11,12
- Clasificación de los datos por separado:
- Method A: 3(3),4(4),2(1.5),6(7.5),2(1.5),5(5.5)
- Method B: 9(11),7(9),5(5.5),10(12),6(1.5),8(10)
- Calculando la suma de rango):
- R1: 3+4+1.5+7.5+1.5+5.5=23
- R2: 11+9+5.5+12+1.5+10=55
Ahora calcule el valor estadístico usando esta fórmula:
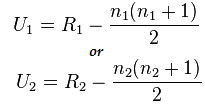
Aquí n1=6 y n2=6
Y el valor después del cálculo para U1=2 y para U2= 34
Calculando la estadística U:
Us= mín(U1,U2)= mín(2,34)= 2
Desde Mesa Mann Whitney podemos encontrar el valor crítico
En este caso el Valor Crítico será 5
Dado que Uc = 5, que es mayor que Us con un nivel de significancia del 5%, rechazamos H0
Por tanto podemos concluir que existe una diferencia entre el Rango de cada tratamiento.
Implementación con Python
from scipy.stats import mannwhitneyu, norm
import numpy as np
TreatmentA = np.array([3,4,2,6,2,5])
TreatmentB = np.array([9,7,5,10,6,8])
# Perform Mann-Whitney U test
U_statistic, p_value = mannwhitneyu(TreatmentA, TreatmentB)
# Print the result
print(f'The U-statistic is {U_statistic:.2f} and the p-value is {p_value:.4f}')
if p_value < 0.05:
print("Reject Null Hypothesis: There is a significant difference between the Rank of each treatment.")
else:
print("Fail to Reject Null Hypothesis: Fail to Reject Null Hypothesis: There is no enough evidence to conclude that there is difference between the Rank of each treatment")Salida:

Prueba de Kruskal-Wallis
La prueba Kruskal-Wallis se utiliza con múltiples grupos. Es la alternativa no paramétrica y valiosa a una prueba ANOVA unidireccional cuando se violan los supuestos de normalidad e igualdad de varianza. La prueba de Kruskal-Wallis compara medianas de más de dos grupos independientes.
Se prueba la Hipótesis Nula cuando se extraen k muestras independientes (k>=3) de una población con distribuciones idénticas, sin requerir la condición de normalidad para las poblaciones.
Supuestos:
Asegúrese de que haya al menos tres muestras aleatorias extraídas de forma independiente. Cada muestra tiene al menos 5 observaciones, n>=5
Considere un ejemplo en el que queremos determinar si la técnica de estudio utilizada por tres grupos de estudiantes afecta sus calificaciones en los exámenes. Podemos utilizar la prueba de Kruskal-Wallis para analizar los datos y evaluar si existen diferencias estadísticamente significativas en las puntuaciones de los exámenes entre los grupos.
Formule la hipótesis nula para esto como:
- H0: No hay diferencia en las puntuaciones de los exámenes entre los tres grupos de estudiantes.
- Ha: Existe una diferencia en las puntuaciones de los exámenes entre los tres grupos de estudiantes.
Prueba de rango con signo de Wilcoxon
La prueba de rangos con signo de Wilcoxon (también conocida como prueba de pares emparejados de Wilcoxon) es la versión no paramétrica de la prueba t de muestras dependientes o de la prueba t de muestras pareadas. La prueba de signos es la otra alternativa no paramétrica a la prueba t de muestras pareadas. Se utiliza cuando las variables de interés son de naturaleza dicotómica (como Hombre y Mujer, Sí y No). La prueba de rango con signo de Wilcoxon también es una versión no paramétrica para la prueba t de una muestra. La prueba de rango con signo de Wilcoxon compara las medianas de los grupos en dos situaciones (muestras pareadas) o compara la mediana del grupo con la mediana hipotética (una muestra).
Entendamos esto con un ejemplo, supongamos que tenemos datos sobre el consumo diario de cigarrillos de los fumadores antes y después de participar en un programa de 8 semanas y queremos determinar si existe una diferencia significativa en el consumo diario de cigarrillos antes y después del programa, entonces usa esta prueba
La formulación de hipótesis para esto será
- H0: No hay diferencia en el consumo diario de cigarrillos antes y después del programa.
- Ha: Existe una diferencia en el consumo diario de cigarrillos antes y después del programa
Prueba de normalidad
Analicemos ahora las pruebas de normalidad:
Prueba de Shapiro Wilk
La prueba de Shapiro-Wilk evalúa si una muestra determinada de datos proviene de una población distribuida normalmente. Es una de las pruebas más utilizadas para comprobar la normalidad. La prueba es particularmente útil cuando se trata de tamaños de muestra relativamente pequeños.
En la prueba de Shapiro-Wilk:
- Hipótesis nula : Los datos de la muestra provienen de una población que sigue una distribución normal.
- Hipótesis alternativa : Los datos de la muestra no provienen de una población que sigue una distribución normal.
El estadístico de prueba generado por la prueba de Shapiro-Wilk mide la discrepancia entre los datos observados y los datos esperados bajo el supuesto de normalidad. Si el valor p asociado con la estadística de prueba es menor que un nivel de significancia elegido (por ejemplo, 0.05), rechazamos la hipótesis nula, lo que indica que los datos no se distribuyen normalmente. Si el valor p es mayor que el nivel de significancia, no podemos rechazar la hipótesis nula, lo que sugiere que los datos pueden seguir una distribución normal.
Primero, creemos un conjunto de datos para estas pruebas. Puede utilizar cualquier conjunto de datos de su elección:
import pandas as pd
# Create the dictionary with the provided data
data = {
'population': [6.1101, 5.5277, 8.5186, 7.0032, 5.8598],
'profit': [17.5920, 9.1302, 13.6620, 11.8540, 6.8233]
}
# Create the DataFrame
df = pd.DataFrame(data)
response_var=df['profit']
Here, a sample for running Shapiro -Wilk test on python:
from scipy.stats import shapiro
stat, p_val = shapiro(response_var)
print(f'Shapiro-Wilk Test: Statistic={stat} p-value={p_val}')
if p_val > alpha:
print('Data looks normal (fail to reject H0)')
else:
print('Data looks normal (fail to reject H0)')Salida:

Esta prueba es más apropiada para tamaños de muestra relativamente pequeños (n = <50-2000), ya que se vuelve menos confiable con tamaños de muestra más grandes.
Anderson-querida
Evalúa si una muestra determinada de datos proviene de una distribución específica, como la distribución normal. Es similar a la prueba de Shapiro-Wilk pero es más sensible, especialmente para muestras de tamaño más pequeño.
Se adapta a varias distribuciones, incluida la distribución normal, en los casos en que se desconocen los parámetros de la distribución.
Aquí, código Python para implementarlo:
from scipy.stats import anderson
response_var = data['profit']
alpha = 0.05
# Anderson-Darling Test
result = anderson(response_var)
print(f'Anderson statistics: {result.statistic:.3f}')
if result.statistic > result.critical_values[-1]:
p_value = 0.0 # The p-value is essentially 0 if the statistic exceeds the largest critical value
else:
p_value = result.significance_level[result.statistic < result.critical_values][-1]
print("P-value:", p_value)
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")Salida:

Prueba de Jarque-Bera
La prueba de Jarque-Bera evalúa si una determinada muestra de datos proviene de una población distribuida normalmente. Se basa en la asimetría y curtosis de los datos.
Aquí está la implementación de Jarque-Bera Test en Python con datos de muestra:
from scipy.stats import jarque_bera
# Performing Jarque-Bera test
test_statistic, p_value = jarque_bera(response_var)
print("Jarque-Bera Test Statistic:", test_statistic)
print("P-value:", p_value)
# Interpreting results
alpha = 0.05
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")Salida:

| Categoría | Técnicas estadísticas paramétricas | Estadística no paramétricaTécnicas |
| correlación | Coeficiente de correlación del momento del producto de Pearson (r) | Correlación del coeficiente de rango de Spearman (Rho), Tau de Kendall |
| Dos grupos, medidas independientes | Prueba t independiente | Prueba U de Mann-Whitney |
| Más de dos grupos, medidas independientes | ANOVA unidireccional | ANOVA unidireccional de Kruskal-Wallis |
| Dos grupos, medidas repetidas | Prueba t pareada | Prueba de rango con signo de par emparejado de Wilcoxon |
| Más de dos grupos, medidas repetidas | ANOVA unidireccional de medidas repetidas | Análisis de varianza bidireccional de Friedman |
Conclusión
Evaluación de la hipótesis Es esencial para evaluar afirmaciones sobre parámetros de población utilizando datos de muestra. Las pruebas paramétricas se basan en supuestos específicos y son adecuadas para datos de intervalo o de razón, mientras que las pruebas no paramétricas son más flexibles y aplicables a datos nominales u ordinales sin supuestos distributivos estrictos. Pruebas como Shapiro-Wilk y Anderson-Darling evalúan la normalidad, mientras que Chi-cuadrado y Jarque-Bera evalúan la bondad de ajuste. Comprender las diferencias entre pruebas paramétricas y no paramétricas es crucial para seleccionar el enfoque estadístico adecuado. En general, las pruebas de hipótesis proporcionan un marco sistemático para tomar decisiones basadas en datos y extraer conclusiones confiables a partir de evidencia empírica.
¿Listo para dominar el análisis estadístico avanzado? ¡Inscríbase hoy en nuestro curso de análisis de datos BlackBelt! Obtenga experiencia en pruebas de hipótesis, pruebas paramétricas y no paramétricas, implementación de Python y más. Mejore sus habilidades estadísticas y sobresalga en la toma de decisiones basada en datos. ¡Únete ahora!
Preguntas frecuentes
R. Las pruebas paramétricas hacen suposiciones sobre la distribución de la población y los parámetros, como la normalidad y la homogeneidad de la varianza, mientras que las pruebas no paramétricas no se basan en estas suposiciones. Las pruebas paramétricas tienen más poder cuando se cumplen los supuestos, mientras que las pruebas no paramétricas son más sólidas y aplicables en una gama más amplia de situaciones, incluso cuando los datos están sesgados o no están distribuidos normalmente.
R. La prueba de chi-cuadrado se utiliza para determinar si existe una asociación significativa entre dos variables categóricas. Comúnmente analiza datos categóricos y prueba hipótesis sobre la independencia de variables en tablas de contingencia.
A. La prueba U de Mann-Whitney compara dos grupos independientes cuando la variable dependiente es ordinal o no tiene una distribución normal. Evalúa si existe una diferencia significativa entre las medianas de los dos grupos.
R. La prueba de Shapiro-Wilk evalúa si una muestra proviene de una población distribuida normalmente. Pone a prueba la hipótesis nula de que los datos siguen una distribución normal. Si el valor p es menor que el nivel de significancia elegido (p. ej., 0.05), rechazamos la hipótesis nula y concluimos que los datos no se distribuyen normalmente.
- Distribución de relaciones públicas y contenido potenciado por SEO. Consiga amplificado hoy.
- PlatoData.Network Vertical Generativo Ai. Empodérate. Accede Aquí.
- PlatoAiStream. Inteligencia Web3. Conocimiento amplificado. Accede Aquí.
- PlatoESG. Carbón, tecnología limpia, Energía, Ambiente, Solar, Gestión de residuos. Accede Aquí.
- PlatoSalud. Inteligencia en Biotecnología y Ensayos Clínicos. Accede Aquí.
- Fuente: https://www.analyticsvidhya.com/blog/2024/04/a-comprehensive-guide-on-non-parametric-tests/



