Introducción

Antes Wordle, el Sudoku estaba de moda y sigue siendo muy popular. En los últimos años, el uso de optimización Los métodos para resolver el rompecabezas han sido un tema dominante. Ver “Resolver Sudoku mediante optimización en Arkieva.

En la actualidad, el uso de la inteligencia artificial (IA) se centra en el aprendizaje automático, que abarca una amplia gama de métodos, desde la regresión con lazo hasta el aprendizaje por refuerzo. El uso de la IA ha resurgió para abordar complejos programación desafíos. Un método, la búsqueda con retroceso, se utiliza habitualmente y es perfecto para el Sudoku.

Este blog proporcionará una descripción detallada sobre cómo utilizar este método para resolver Sudoku. Resulta que el "retroceso" se puede encontrar dentro de los motores de optimización y aprendizaje automático y es una piedra angular de la heurística avanzada que Arkieva utiliza para la programación. El algoritmo se implementa en un "lenguaje de programación de matrices", un lenguaje de programación orientado a funciones que maneja un rico conjunto de estructuras de matriz.

Conceptos básicos del sudoku

De Wikipedia: Sudoku es un rompecabezas combinatorio de colocación de números basado en la lógica. El objetivo es llenar una cuadrícula de 9×9 con dígitos para que cada columna, cada fila y cada una de las nueve subcuadrículas de 3×3 que componen la cuadrícula (también llamadas “cuadros”, “bloques”, “regiones”, o “subcuadrados”) contiene todos los dígitos del 1 al 9. El creador de rompecabezas proporciona una cuadrícula parcialmente completa, que generalmente tiene una solución única. Los rompecabezas completados son siempre una especie de cuadrado latino con una restricción adicional en el contenido de las regiones individuales. Por ejemplo, el mismo número entero no puede aparecer dos veces en la misma fila o columna del tablero de juego de 9×9 o en cualquiera de las nueve subregiones de 3×3 del tablero de juego de 9×9.

La Tabla 1 tiene un problema de ejemplo. Hay 9 filas y 9 columnas para un total de 81 celdas. A cada uno se le permite tener uno y sólo uno de nueve números enteros entre 1 y 9. En la solución inicial, una celda tiene un valor único, que fija el valor de esta celda en ese valor, o la celda está en blanco, lo que indica que necesitamos para encontrar un valor para esta celda. La celda (1,1) tiene el valor 2 y la celda (6,5) tiene el valor 6. Las celdas (1,2) y (2,3) están en blanco y el algoritmo encontrará un valor para estas celdas.

la complicación

Además de pertenecer a una y sólo una fila y columna, una celda pertenece a una y sólo 1 casilla. Hay 9 cuadros y están indicados por color en la Tabla 1. La Tabla 2 utiliza un número entero único entre 1 y 9 para identificar cada cuadro o cuadrícula. Las celdas con un valor de fila de (1, 2 o 3) y un valor de columna de (1, 2 o 3) pertenecen al cuadro 1. El cuadro 6 son valores de fila de (4, 5, 6) y valores de columna (7, 8 , 9). La identificación de la caja está determinada por la fórmula BOX_ID = {3x(floor((ROW_ID-1) /3)} + techo (COL_ID/3). Para la celda (5,7), 6 = 3x(floor(5-1 ))/3) + techo (8/3)= 3×1 + 3 = 3+3.

El corazón del rompecabezas

Encontrar un valor entero entre 1 y 9 para cada celda desconocida de modo que los números enteros del 1 al 9 se usen una vez y solo una vez para cada columna, cada fila y cada cuadro.

Miremos la celda (1,3) que está en blanco. La fila 1 ya tiene los valores 2 y 7. Estos no están permitidos en esta celda. La columna 3 ya tiene los valores 3, 5,6, 7,9. Estos no están permitidos. La casilla 1 (amarilla) tiene los valores 2, 3 y 8. Estos no están permitidos. No se permiten los siguientes valores (2,7); (3, 5, 6, 7, 9); (2, 3, 8). Los valores únicos no permitidos son (2, 3, 5, 6, 7, 8, 9). Los únicos valores candidatos son (1,4).

Una solución sería asignar temporalmente 1 a la celda (1,3) y luego intentar encontrar valores candidatos para otra celda.

Una solución de retroceso: componentes iniciales

Estructura de matriz

El punto de partida es decidir una estructura de matriz para almacenar el problema fuente y respaldar la búsqueda. La Tabla 3 tiene esta estructura de matriz. La columna 1 es una identificación entera única para cada celda. Los valores oscilan entre 1 y 81. La columna 2 es el ID de fila de la celda. La columna 3 es el ID de columna de la celda. La columna 4 es la identificación del cuadro. La columna 5 es el valor en la celda. Observe que a una celda sin valor se le asigna el valor cero en lugar de blanco o nulo. Esto mantiene esto como una “matriz de solo números enteros”, muy superior en cuanto a rendimiento.

En APL, esta matriz se almacenaría en una matriz bidimensional donde la forma es de 2 por 81. Suponga que los elementos de la Tabla 5 están almacenados en la variable MAT. Las funciones de ejemplo son:

El comando MAT[1 2 3;] toma las primeras 3 filas de MAT
1 1 1 1 2
2 1 2 1 0
3 1 3 1 0
MAT[1 2 3; 4 5] asegura las filas 1, 2, 3 y solo las columnas 4 y 5
1 2
1 0
1 0
(MAT[;5]=0)/MAT[;1] encuentra todas las celdas que necesitan un valor.

INSERTAR TABLA 3

Comprobación de cordura: duplicados

¡Antes de comenzar la búsqueda, es fundamental realizar una verificación de cordura! Ésa es la solución inicial factible. Es factible para Sudoku si ahora hay duplicados en cualquier fila, columna o cuadro. La solución inicial actual, por ejemplo 1, es factible. La Tabla 4 tiene un ejemplo donde la solución inicial tiene duplicados. La fila 1 tiene dos valores 2. El área 1 tiene dos valores 2. La función “SANITY_DUPE” maneja esta lógica.

Verificación de cordura: opciones para celdas sin valores

Una información muy útil serían todos los valores posibles para una celda sin valor. Si no hay candidatos, entonces este rompecabezas no tiene solución. Una celda no puede tomar un valor que ya reclama su vecina. Usando la Tabla 1 para la celda (1,3,'1' – este último 1 es el boxid), sus vecinos son la fila 1, la columna 3 y el cuadro 1. La fila 1 tiene los valores (2,7); la columna 3 tiene los valores (3,5,6,7,9); el cuadro 1 tiene los valores (2,3,8). La celda (1,3.1) no puede tomar los siguientes valores (2,3,5,6,7,8,9). Las únicas opciones para la celda (1,3,1) son (1,4). Para la celda (4,1,2), los valores 1, 2, 3, 5, 6, 7, 9 ya se utilizan en la fila 4, columna 1 y/o cuadro 4. Los únicos valores candidatos son (4,8) . La función "SANITY_CAND" maneja esta lógica.

La Tabla 5 muestra los candidatos, por ejemplo, 1 al inicio del proceso de búsqueda. Si a una celda ya se le ha asignado un valor en las condiciones iniciales (Tabla 1), entonces este valor se repite y se muestra en rojo. Si una celda que necesita un valor tiene solo una opción, ésta se muestra en blanco. La celda (8,7,9) tiene el valor único 7 en blanco. (2,5,8,4,3) son reclamados por la columna vecina 7. (1, 2, 9) por la fila 8. (3,2,6) por el cuadro 9. Sólo el valor 7 no está reclamado.

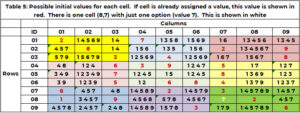
Control de cordura: buscando conflictos

La información que identifica todas las opciones para las celdas que necesitan un valor (publicada en la Tabla 4) nos permite identificar un conflicto antes de iniciar el proceso de búsqueda. Se produce un conflicto cuando dos celdas que necesitan un valor tienen solo un candidato, el valor del candidato es el mismo y las dos celdas son vecinas. De la Tabla 4 sabemos que la única celda que necesita un valor y tiene un solo candidato es la celda (8,7,9). Por ejemplo 1, no hay conflicto.

¿Qué sería un conflicto? Si el único valor posible para la celda (3,7,3) era 7 (en lugar de 1, 6, 7), entonces hay un conflicto. La celda (8,7) y la celda (3,7) son vecinas: la misma columna. Sin embargo, si el único valor posible para la celda (4,9,2) fuera 7 (en lugar de 1, 2, 7), esto no sería un conflicto. Estas células no son vecinas.

Resumen de verificación de cordura

1. Si hay duplicados, la solución inicial no es factible.
2. Si una celda que necesita un valor no tiene ningún candidato, entonces no hay solución posible para este rompecabezas. La lista de valores candidatos para cada celda se puede utilizar para reducir el espacio de búsqueda, tanto para retroceder como para optimizar.
3. La capacidad de encontrar conflictos identifica que el enigma no es factible –no tiene solución– sin un proceso de búsqueda. Además, identifica las "células problemáticas".

Una solución de retroceso: proceso de búsqueda

Una vez implementadas las estructuras de datos centrales y la verificación de la cordura, centramos nuestra atención en el proceso de búsqueda. El tema recurrente es, nuevamente, implementar estructuras de datos para respaldar la búsqueda.

Seguimiento de la búsqueda

La matriz Seguimiento realiza un seguimiento de las tareas realizadas

1. La columna 1 es el contador.
2. Col 2 es el número de opciones disponibles para asignar a esta celda
   • 1 significa 1 opción disponible, 2 significa dos opciones, etc.
   • 0 significa: no hay opción disponible o se restablece a 0 (sin valor asignado) y retrocede
3. La columna 3 es la celda a la que se le asigna un número de índice de valor (1 a 81)
4. La columna 4 es el valor asignado a la celda en el historial de seguimiento.
   • Un valor de 9999 significa que esta celda estaba cuando se encontró el callejón sin salida.
   • El valor de un número entero entre 1 y 9 inclusive, es el valor asignado a esta celda en este punto del proceso de búsqueda.
   • Un valor de 0 significa que esta celda necesita una asignación

La matriz de seguimiento se utiliza para respaldar el proceso de búsqueda. la matriz HISTORIA DE PISTA Tiene la misma estructura que el rastreador pero mantiene el historial de todo el proceso de búsqueda. La Tabla 6 tiene parte de TRACKHIST, por ejemplo 1. Se explica con más detalle en una sección posterior.

Además, la matriz Pav (un vector de un vector), realiza un seguimiento de los valores previamente asignados a esta celda. Esto garantiza que no volvamos a visitar una solución fallida, similar a lo que se hace en TABU.

Hay un proceso de registro opcional donde el proceso de búsqueda escribe cada paso.

Iniciando la búsqueda

Una vez realizadas la contabilidad y la comprobación de la cordura, ahora podemos iniciar el proceso de búsqueda. Los pasos son:

1. ¿Quedan celdas que necesiten un valor? – si no, entonces hemos terminado.
2. Para cada celda que necesite un valor, busque todas las opciones candidatas para cada celda. La Tabla 4 tiene estos valores al inicio del proceso de solución. En cada iteración, esto se actualiza para dar cabida a los valores asignados a las celdas.
3. Evalúe las opciones en este orden.
   • Si una celda tiene CERO opciones, entonces instituya el retroceso
   • Busque todas las celdas con una opción, seleccione una de estas celdas, realice esta asignación,
     1. y actualizar la tabla de seguimiento, la solución actual y PAV.
   • Si todas las celdas tienen más de una opción, seleccione una celda y un valor y actualice
     1. y actualizar la tabla de seguimiento, la solución actual y PAV

Usaremos la Tabla 6, que es parte de la historia del proceso de solución (llamada TRACKHIST) para ilustrar cada paso.

En la primera iteración (CTR=1), se selecciona la celda 70 (fila 8, columna 7, cuadro 9) para asignarle un valor. Solo existe el candidato (7), y este valor se asigna a la celda 70. Además, el valor 7 se suma al vector de valores previamente asignados (PAV) para la celda 70.

En la segunda iteración, a la celda 30 se le asigna el valor 1. Esta celda tenía dos valores candidatos. El valor candidato más pequeño se asigna a la celda (solo una regla arbitraria para que la lógica sea fácil de seguir).

El proceso de identificar una celda que necesita un valor y asignar un valor funciona bien hasta la iteración (CTR) 20. La celda 9 necesita valor, pero el número de candidatos es CERO. Hay dos opciones:

• No hay solución para este enigma.
• Deshacemos (retrocedemos) algunas de las asignaciones y tomamos otro camino.

Buscamos la asignación de celda más cercana a esta, donde había más de una opción. En este ejemplo, esto ocurrió en la iteración 18, donde a la celda 5 se le asigna el valor 3, pero había dos valores candidatos para la celda 5: los valores 3 y 8.

Entre la celda 5 (CTR = 18) y la celda 9 (CTR = 20), a la celda 8 se le asigna el valor 4 (CTR = 19). Volvemos a colocar las celdas 8 y 5 en la lista "necesita un valor". Esto se captura en la segunda y tercera entrada CTR=20, donde el valor se establece en 0. El valor 3 se mantiene en el vector PAV para la celda 5. Es decir, el motor de búsqueda no puede asignar el valor 3 a la celda 5.

El motor de búsqueda se inicia nuevamente para identificar un valor para la celda 5 (con 3 ya no es una opción) y asigna el valor 8 a la celda 5 (CTR=21). Continúa hasta que todas las celdas tengan un valor o haya una celda sin opción y no haya una ruta de retroceso. La solución se publica en la Tabla 7.

Observe que cuando hay más de un candidato para una celda, esta es una oportunidad para el procesamiento paralelo.

Comparación con la solución de optimización MILP

A nivel superficial, la representación del Sudoku es dramáticamente diferente. El enfoque de IA utiliza números enteros y, desde cualquier punto de vista, es una representación más ajustada e intuitiva. Además, los verificadores de cordura brindan información útil para crear una formulación más sólida. La representación MILP es infinita binarios (0/1). Sin embargo, los binarios son representaciones poderosas dada la solidez de los solucionadores MILP modernos.

Sin embargo, internamente, el solucionador MILP no conserva los binarios sino que utiliza un método de matriz dispersa para eliminar el almacenamiento de todos los ceros. Además, los algoritmos para resolver binarios no surgen hasta las décadas de 1980 y 1990. El artículo de 1983 de Crowder, Johnson y Padberg informa sobre una de las primeras soluciones prácticas de optimización con binarios. Señalan la importancia de un preprocesamiento inteligente y de métodos de bifurcación y vinculación como fundamentales para una solución exitosa.

La reciente explosión del uso de programación y software restringidos como solucionador local ha dejado clara la importancia de utilizar métodos de IA con los métodos de optimización originales como la programación lineal y los mínimos cuadrados.

• Distribución de relaciones públicas y contenido potenciado por SEO. Consiga amplificado hoy.
• PlatoData.Network Vertical Generativo Ai. Empodérate. Accede Aquí.
• PlatoAiStream. Inteligencia Web3. Conocimiento amplificado. Accede Aquí.
• PlatoESG. Carbón, tecnología limpia, Energía, Ambiente, Solar, Gestión de residuos. Accede Aquí.
• PlatoSalud. Inteligencia en Biotecnología y Ensayos Clínicos. Accede Aquí.
• Fuente: https://blog.arkieva.com/an-artificial-intelligence-based-solution-to-sudoku/?utm_source=rss&utm_medium=rss&utm_campaign=an-artificial-intelligence-based-solution-to-sudoku