Los informáticos son un grupo exigente. Para ellos, no es suficiente obtener la respuesta correcta a un problema; el objetivo, casi siempre, es obtener la respuesta de la manera más eficiente posible.

Tomemos como ejemplo el acto de multiplicar matrices o conjuntos de números. En 1812, el matemático francés Jacques Philippe Marie Binet ideó el conjunto básico de reglas que todavía enseñamos a los estudiantes. Funciona perfectamente, pero otros matemáticos han encontrado formas de simplificar y acelerar el proceso. Ahora la tarea de acelerando el proceso La multiplicación de matrices se encuentra en la intersección de las matemáticas y la informática, donde los investigadores continúan mejorando el proceso hasta el día de hoy, aunque en las últimas décadas los avances han sido bastante modestos. Desde 1987, las mejoras numéricas en la multiplicación de matrices han sido "pequeñas y... extremadamente difíciles de obtener", dijo François Le Gall, informático de la Universidad de Nagoya.

Ahora, tres investigadores (Ran Duan y Renfei Zhou de la Universidad de Tsinghua y Hongxun Wu de la Universidad de California en Berkeley) han dado un gran paso adelante para atacar este problema perenne. Su nuevos resultados, presentado en noviembre pasado en la conferencia Foundations of Computer Science, surge de una nueva técnica inesperada, dijo Le Gall. Aunque la mejora en sí fue relativamente pequeña, Le Gall la calificó de “conceptualmente mayor que otras anteriores”.

La técnica revela una fuente de posibles mejoras hasta ahora desconocida y, por tanto, sin explotar, y ya ha dado sus frutos: un segundo documento, publicado en enero, se basa en el primero para mostrar cómo se puede impulsar aún más la multiplicación de matrices.

"Este es un gran avance técnico", dijo William Kuszmaul, un informático teórico de la Universidad de Harvard. "Es la mayor mejora en la multiplicación de matrices que hemos visto en más de una década".

Entra en la matriz

Puede parecer un problema oscuro, pero la multiplicación de matrices es una operación computacional fundamental. Está incorporado en una gran proporción de los algoritmos que la gente usa todos los días para una variedad de tareas, desde mostrar gráficos de computadora más nítidos hasta resolver problemas logísticos en teoría de redes. Y como en otras áreas de la computación, la velocidad es primordial. Incluso pequeñas mejoras podrían eventualmente conducir a importantes ahorros de tiempo, poder computacional y dinero. Pero por ahora, los teóricos están interesados ​​principalmente en descubrir qué tan rápido puede llegar a ser el proceso.

La forma tradicional de multiplicar dos. n-Por-n matrices (multiplicando números de cada fila de la primera matriz por números de las columnas de la segunda) requiere n³ multiplicaciones separadas. Para matrices de 2 por 2, eso significa 2³ u 8 multiplicaciones.

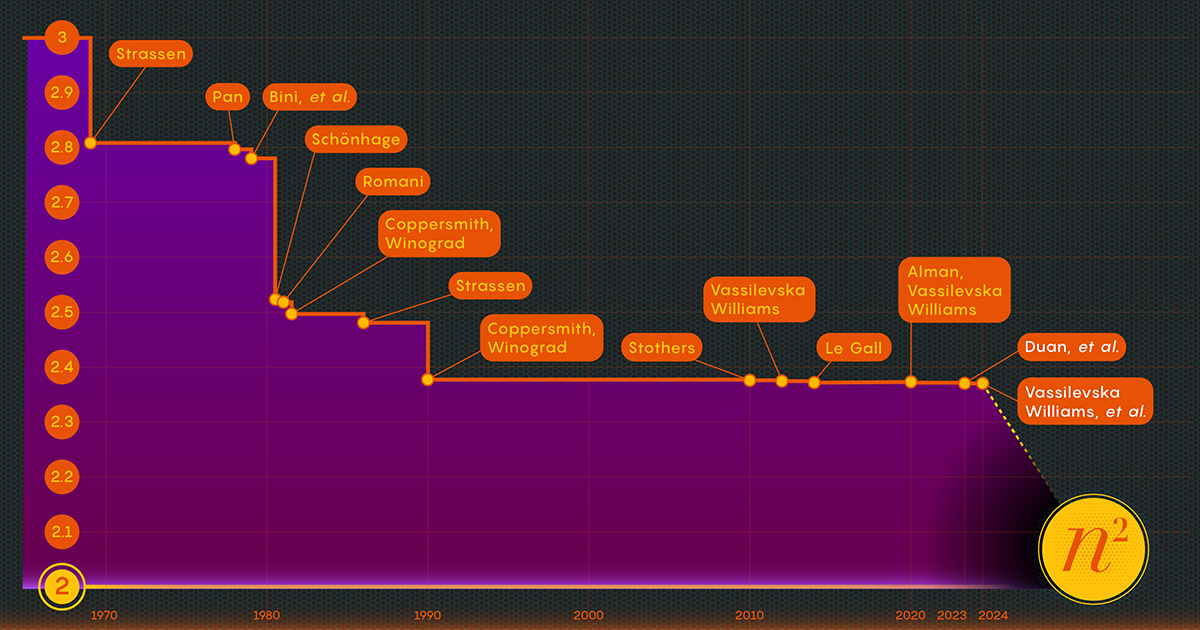
En 1969, el matemático Volker Strassen reveló un procedimiento más complicado que podía multiplicar matrices de 2 por 2 en sólo siete pasos multiplicativos y 18 sumas. Dos años más tarde, el informático Shmuel Winograd demostró que siete es, efectivamente, el mínimo absoluto para matrices de 2 por 2.

Strassen explotó esa misma idea para demostrar que todos los grandes n-Por-n Las matrices también se pueden multiplicar en menos de n³ pasos. Un elemento clave de esta estrategia implica un procedimiento llamado descomposición: dividir una matriz grande en submatrices sucesivamente más pequeñas, que podrían terminar siendo tan pequeñas como 2 por 2 o incluso 1 por 1 (estos son solo números únicos).

La razón para dividir una matriz gigante en pedazos pequeños es bastante simple, según Virginia Vassilevska Williams, científico informático del Instituto de Tecnología de Massachusetts y coautor de uno de los nuevos artículos. "Es difícil para un ser humano mirar una matriz grande (digamos, del orden de 100 por 100) y pensar en el mejor algoritmo posible", dijo Vassilevska Williams. Ni siquiera las matrices de 3 por 3 se han resuelto por completo todavía. "Sin embargo, se puede utilizar un algoritmo rápido que ya se haya desarrollado para matrices pequeñas para obtener también un algoritmo rápido para matrices más grandes".

La clave para la velocidad, según han determinado los investigadores, es reducir el número de pasos de multiplicación, bajando ese exponente de n³ (para el método estándar) tanto como puedan. El valor más bajo posible, n², es básicamente lo que lleva escribir la respuesta. Los científicos informáticos se refieren a ese exponente como omega, ω, con n^ω siendo el menor número posible de pasos necesarios para multiplicar con éxito dos n-Por-n matrices como n crece muy grande. "El objetivo de este trabajo", dijo Zhou, quien también fue coautor del artículo de enero de 2024, "es ver qué tan cerca se puede llegar a 2 y si se puede lograr en teoría".

Un enfoque láser

En 1986, Strassen logró otro gran avance cuando Introducido lo que se llama el método láser para la multiplicación de matrices. Strassen lo utilizó para establecer un valor superior de omega de 2.48. Si bien el método es sólo un paso en las multiplicaciones de matrices grandes, es uno de los más importantes porque los investigadores han seguido mejorándolo.

Un año después, Winograd y Don Coppersmith introdujeron un nuevo algoritmo que complementaba maravillosamente el método láser. Esta combinación de herramientas ha aparecido en prácticamente todos los esfuerzos posteriores para acelerar la multiplicación de matrices.

He aquí una forma simplificada de pensar en cómo encajan estos diferentes elementos. Comencemos con dos matrices grandes, A y B, que deseas multiplicar. Primero, se descomponen en muchas submatrices o bloques más pequeños, como a veces se les llama. A continuación, puede utilizar el algoritmo de Coppersmith y Winograd como una especie de manual de instrucciones para manipular y, en última instancia, ensamblar los bloques. "Me dice qué multiplicar y qué sumar y qué entradas van y dónde" en la matriz de producto C, dijo Vassilevska Williams. "Es sólo una receta para construir C a partir de A y B".

Sin embargo, hay un problema: a veces terminas con bloques que tienen entradas en común. Dejarlos en el producto sería como contar esas entradas dos veces, por lo que en algún momento tendrás que deshacerte de esos términos duplicados, llamados superposiciones. Los investigadores hacen esto "matando" los bloques en los que se encuentran: igualando sus componentes a cero para eliminarlos del cálculo.

Aquí es donde finalmente entra en juego el método láser de Strassen. "El método láser normalmente funciona muy bien y generalmente encuentra una buena manera de matar un subconjunto de bloques para eliminar la superposición", dijo Le Gall. Después de que el láser haya eliminado o “quemado” todas las superposiciones, puede construir la matriz del producto final, C.

La combinación de estas diversas técnicas da como resultado un algoritmo para multiplicar dos matrices con un número general deliberadamente reducido de multiplicaciones, al menos en teoría. El método láser no pretende ser práctico; es sólo una forma de pensar en la forma ideal de multiplicar matrices. "Nunca ejecutamos el método [en una computadora]", dijo Zhou. "Lo analizamos".

Y ese análisis es lo que condujo a la mayor mejora de omega en más de una década.

Se encuentra una pérdida

El artículo del verano pasado, escrito por Duan, Zhou y Wu, demostró que el proceso de Strassen aún podría acelerarse significativamente. Todo se debió a un concepto que llamaron pérdida oculta, enterrado profundamente en análisis anteriores: "el resultado de matar involuntariamente demasiados bloques", dijo Zhou.

El método láser funciona etiquetando bloques superpuestos como basura, programados para su eliminación; otros bloques se consideran dignos y se salvarán. El proceso de selección, sin embargo, es algo aleatorio. Un bloque clasificado como basura puede, de hecho, resultar útil después de todo. Esto no fue una sorpresa total, pero al examinar muchas de estas elecciones aleatorias, el equipo de Duan determinó que el método láser estaba infravalorando sistemáticamente los bloques: se debían guardar más bloques y desechar menos. Y, como suele ocurrir, menos desperdicio se traduce en mayor eficiencia.

"Poder mantener más bloques sin superposición conduce a... un algoritmo de multiplicación de matrices más rápido", dijo Le Gall.

Tras comprobar la existencia de esta pérdida, el equipo de Duan modificó la forma en que el método láser etiquetaba los bloques, reduciendo sustancialmente el desperdicio. Como resultado, establecieron un nuevo límite superior para omega en alrededor de 2.371866, una mejora con respecto al límite superior anterior de 2.3728596. ambientado en 2020 por Josh Alman y Vassilevska Williams. Esto puede parecer un cambio modesto, ya que reduce el límite en aproximadamente 0.001. Pero es la mayor mejora que los científicos han visto desde 2010. El resultado de Vassilevska Williams y Alman en 2020, en comparación, solo mejoró con respecto a su predecesor en 0.00001.

Pero lo más emocionante para los investigadores no es sólo el nuevo registro en sí, que no duró mucho. También es el hecho de que el artículo reveló una nueva vía de mejora que, hasta entonces, había pasado totalmente desapercibida. Desde hace casi cuatro décadas, todo el mundo confía en el mismo método láser, afirmó Le Gall. “Luego descubrieron que, bueno, podemos hacerlo mejor”.

El artículo de enero de 2024 perfeccionó este nuevo enfoque, lo que permitió a Vassilevska Williams, Zhou y sus coautores reducir aún más la pérdida oculta. Esto llevó a una mejora adicional del límite superior de omega, reduciéndolo a 2.371552. Los autores también generalizaron esa misma técnica para mejorar el proceso de multiplicación de rectangular (n-Por-m) matrices: un procedimiento que tiene aplicaciones en teoría de grafos, aprendizaje automático y otras áreas.

Es casi seguro que se producirán más avances en este sentido, pero existen límites. En 2015, Le Gall y dos colaboradores demostrado que el enfoque actual (el método láser junto con la receta Coppersmith-Winograd) no puede producir un omega por debajo de 2.3078. Para realizar más mejoras, dijo Le Gall, “es necesario mejorar el [enfoque] original de Coppersmith y Winograd que realmente no ha cambiado desde 1987.." Pero hasta ahora a nadie se le ha ocurrido una forma mejor. Puede que ni siquiera haya uno.

"Mejorar el omega es en realidad parte de la comprensión de este problema", dijo Zhou. “Si podemos comprender bien el problema, podremos diseñar mejores algoritmos para solucionarlo. [Y] la gente todavía se encuentra en las primeras etapas de comprensión de este antiguo problema”.