¿Qué es la regresión lineal?

La regresión lineal es la forma básica de análisis de regresión. Asume que existe una relación lineal entre la variable dependiente y los predictores. En la regresión, tratamos de calcular la línea de mejor ajuste, que describe la relación entre los predictores y las variables predictivas/dependientes.

Hay cuatro supuestos asociados con un modelo de regresión lineal:

1. Linealidad: La relación entre las variables independientes y la media de la variable dependiente es lineal. 
2. Homocedasticidad: La varianza de los residuos debe ser igual.
3. Independencia: Las observaciones son independientes entre sí.
4. Normalidad: La variable dependiente se distribuye normalmente para cualquier valor fijo de una variable independiente.

¿No es la regresión lineal de las estadísticas?

Antes de profundizar en los detalles de la regresión lineal, es posible que se pregunte por qué estamos analizando este algoritmo.

¿No es una técnica de la estadística? Aprendizaje automático, más específicamente el campo del modelado predictivo, se preocupa principalmente por minimizar el error de un modelo o hacer las predicciones más precisas posibles a expensas de la explicabilidad. En aprendizaje automático aplicado, tomaremos prestados y reutilizaremos algoritmos de muchos campos diferentes, incluidas las estadísticas, y los usaremos para estos fines.

Como tal, la regresión lineal se desarrolló en el campo de la estadística y se estudia como un modelo para comprender la relación entre las variables numéricas de entrada y salida. Sin embargo, ha sido tomado prestado por el aprendizaje automático y es tanto un algoritmo estadístico como un algoritmo de aprendizaje automático.

Representación del modelo de regresión lineal

La regresión lineal es un modelo atractivo porque la representación es muy simple.
La representación es una ecuación lineal que combina un conjunto específico de valores de entrada (x), cuya solución es la salida predicha para ese conjunto de valores de entrada (y). Como tal, tanto los valores de entrada (x) como el valor de salida son numéricos.

La ecuación lineal asigna un factor de escala a cada valor de entrada o columna, llamado coeficiente y representado por la letra griega mayúscula Beta (B). Un coeficiente adicional es añadido, dando a la línea un grado adicional de libertad (por ejemplo, moviéndose hacia arriba y hacia abajo en una gráfica bidimensional) y a menudo se le llama intersección o coeficiente de sesgo.

Por ejemplo, en un problema de regresión simple (una sola x y una sola y), la forma del modelo sería:
Y= β0 + β1x

En dimensiones superiores, la línea se llama plano o bombo.r-plano cuando tenemos más de una entrada (x). La representación, por lo tanto, tiene la forma de la ecuación y los valores específicos utilizados para los coeficientes (p. ej., β0 y β1 en el ejemplo anterior).

Rendimiento de la regresión

El rendimiento del modelo de regresión se puede evaluar utilizando varias métricas como MAE, MAPE, RMSE, R-squared, etc.

Error absoluto medio (MAE)

Al usar MAE, calculamos la diferencia absoluta promedio entre los valores reales y los valores pronosticados. 

Error de porcentaje absoluto medio (MAPE) 

MAPE se define como el promedio de la desviación absoluta del valor predicho del valor real. Es el promedio de la relación de la diferencia absoluta entre los valores reales y previstos y los valores reales. 

Error cuadrático medio (RMSE)

RMSE calcula el promedio de la raíz cuadrada de la suma de la diferencia al cuadrado entre los valores reales y predichos.

valores R-cuadrado

El valor R-cuadrado representa el porcentaje de la variación en la variable dependiente explicada por la variable independiente en el modelo. 

RSS = Suma residual de cuadrados: Mide la diferencia entre la salida esperada y la real. Un RSS pequeño indica un ajuste estrecho del modelo a los datos. También se define de la siguiente manera: 

TSS = Suma total de cuadrados: Es la suma de los errores de los puntos de datos de la media de la variable de respuesta. 

R² el valor varía de 0 a 1. Cuanto mayor sea el valor de R-cuadrado, mejor será el modelo. El valor de R2 aumenta si añadimos más variables al modelo, independientemente de si la variable contribuye o no al modelo. Esta es la desventaja de usar R².

Valores de R-cuadrado ajustados

El valor de R2 ajustado corrige la desventaja de R2. El valor de R2 ajustado mejorará solo si la variable agregada contribuye significativamente al modelo, y el valor de R ajustado² El valor agrega una penalización al modelo.

donde R² es el valor R-cuadrado, n = el número total de observaciones y k = el número total de variables utilizadas en el modelo, si aumentamos el número de variables, el denominador se vuelve más pequeño y la relación general será alta. Restar de 1 reducirá la R ajustada general². Entonces, para aumentar la R ajustada², la contribución de las características aditivas al modelo debería ser significativamente alta.

Ejemplo de regresión lineal simple

Para la ecuación dada para la regresión lineal,

Si solo hay 1 predictor disponible, se conoce como Regresión lineal simple. 

Al ejecutar la predicción, hay un término de error asociado con la ecuación.

El modelo SLR tiene como objetivo encontrar los valores estimados de β₁ & β₀ manteniendo el término de error (ε) mínimo.

Ejemplo de regresión lineal múltiple

Contribuido por: Rakesh Lakalla
Perfil de Linkedin: https://www.linkedin.com/in/lakkalarakesh/

Para la ecuación dada de regresión lineal,

si hay más de 1 predictor disponible, se conoce como regresión lineal múltiple. 

La ecuación para MLR será:

β₁ = coeficiente para X₁ variable

β₂ = coeficiente para X₂ variable

β₃ = coeficiente para X₃ variable y así sucesivamente...

β₀ es el intercepto (término constante). Al hacer la predicción, hay un término de error asociado con la ecuación.

El objetivo del modelo MLR es encontrar los valores estimados de β_0, β_1, β_2, β_{3 ...} manteniendo el término de error (i) mínimo.

En términos generales, los algoritmos de aprendizaje automático supervisado se clasifican en dos tipos:

1. Regresión: se utiliza para predecir una variable continua
2. Clasificación: se utiliza para predecir variables discretas 

En esta publicación, discutiremos una de las técnicas de regresión, "Regresión lineal múltiple", y su implementación usando Python.

La regresión lineal es uno de los métodos estadísticos del análisis predictivo para predecir la variable objetivo (variable dependiente). Cuando tenemos una variable independiente, la llamamos Regresión lineal simple. Si el número de variables independientes es más de uno, lo llamamos Regresión Lineal Múltiple.

Supuestos para la regresión lineal múltiple

1. Linealidad Debe haber una relación lineal entre las variables dependientes e independientes, como se muestra en el siguiente gráfico de ejemplo.

2. Multicolinealidad: No debe haber una alta correlación entre dos o más variables independientes. La multicolinealidad se puede verificar utilizando una matriz de correlación, Tolerancia y factor de influencia de la varianza (VIF).

3. Homocedasticidad: Si la varianza de los errores es constante en las variables independientes, entonces se llama homocedasticidad. Los residuos deben ser homocedásticos. Los residuos estandarizados frente a los valores predichos se utilizan para verificar la homocedasticidad, como se muestra en la siguiente figura. Las pruebas de Breusch-Pagan y White son las famosas pruebas utilizadas para comprobar la homocedasticidad. Los diagramas QQ también se utilizan para comprobar la homocedasticidad.

4. Normalidad multivariante: Los residuos deben distribuirse normalmente.

5. Datos categóricos: Cualquier dato categórico presente debe convertirse en variables ficticias.

6. Registros mínimos: Debe haber al menos 20 registros de variables independientes.

Una formulación matemática de regresión lineal múltiple

En la regresión lineal, tratamos de encontrar una relación lineal entre las variables independientes y dependientes mediante el uso de una ecuación lineal en los datos.

La ecuación para una línea lineal es-

Y = mx + c

Donde m es la pendiente y c es la intersección.

En la regresión lineal, en realidad estamos tratando de predecir los mejores valores de m y c para la variable dependiente Y y la variable independiente x. Ajustamos la mayor cantidad de líneas y tomamos la mejor línea que da el menor error posible. Usamos los valores de m y c correspondientes para predecir el valor de y.

El mismo concepto se puede utilizar en la regresión lineal múltiple donde tenemos múltiples variables independientes, x1, x2, x3…xn.

Ahora la ecuación cambia a- 

Y=M1X1 + M2X2 + M3M3 + …MnXn+C

La ecuación anterior no es una línea sino un plano de múltiples dimensiones.

Evaluación del modelo:

Un modelo se puede evaluar utilizando los siguientes métodos:

1. Error absoluto medio: Es la media de los valores absolutos de los errores, formulada como: 

1. Error medio cuadrado: Es la media del cuadrado de los errores.

1. Error cuadrático medio de la raíz: Es solo la raíz cuadrada de MSE.

Aplicaciones

1. Se puede calcular el efecto de la variable independiente sobre la variable dependiente.
2. Se utiliza para predecir tendencias.
3. Se usa para encontrar cuánto cambio se puede esperar en una variable dependiente con cambio en una variable independiente.

Regresión polinomial

La regresión polinomial es una regresión no lineal. En la regresión polinomial, la relación de la variable dependiente se ajusta al grado n de la variable independiente. 

Ecuación de regresión polinomial: 

Underfitting y Overfitting

Cuando ajustamos un modelo, tratamos de encontrar la línea optimizada que mejor se ajusta, que puede describir el impacto del cambio en la variable independiente sobre el cambio en la variable dependiente manteniendo el término de error mínimo. Mientras se ajusta el modelo, puede haber 2 eventos que conducirán al mal desempeño del modelo. estos eventos son

1. Adecuado 
2. Sobreajuste

Adecuado 

El ajuste insuficiente es la condición en la que el modelo no puede ajustar los datos lo suficientemente bien. El modelo sub-ajustado conduce a una baja precisión del modelo. Por lo tanto, el modelo no puede capturar la relación, tendencia o patrón en los datos de entrenamiento. El ajuste insuficiente del modelo podría evitarse utilizando más datos u optimizando los parámetros del modelo.

Sobreajuste

El sobreajuste es el caso opuesto al de ajuste insuficiente, es decir, cuando el modelo predice muy bien sobre datos de entrenamiento y no es capaz de predecir bien sobre datos de prueba o datos de validación. La razón principal del sobreajuste podría ser que el modelo está memorizando los datos de entrenamiento y no puede generalizarlos en un conjunto de datos de prueba/no visto. El sobreajuste se puede reducir haciendo una selección de características o usando técnicas de regularización. 

Los gráficos anteriores representan los 3 casos del rendimiento del modelo. 

Implementando Regresión Lineal en Python

Contribuido por: Sra. Manorama Yadav
LinkedIn: https://www.linkedin.com/in/manorama-3110/

Introducción al conjunto de datos

Los datos se refieren al consumo de combustible del ciclo urbano en millas por galón (mpg) que se va a predecir. Hay un total de 392 filas, 5 variables independientes y 1 variable dependiente. Los 5 predictores son variables continuas.

 Información de atributo:

1. millas por galón: continuo (Variable dependiente)
2. cilindros: discreto multivalor
3. desplazamiento: Continuo
4. caballos de fuerza: continua
5. peso: Continuo
6. aceleración: Continua

El objetivo del enunciado del problema es predecir las millas por galón utilizando el modelo de regresión lineal.

Paquetes de Python para regresión lineal

Importe el paquete de Python necesario para realizar varios pasos, como la lectura de datos, el trazado de datos y la realización de una regresión lineal. Importar los siguientes paquetes:

Leer los datos

Descargue los datos y guárdelos en el directorio de datos de la carpeta del proyecto.

Regresión lineal simple con scikit-learn

La regresión lineal simple tiene solo 1 variable predictora y 1 variable dependiente. A partir del conjunto de datos anterior, consideremos el efecto de los caballos de fuerza en el 'mpg' del vehículo.

Echemos un vistazo a cómo se ven los datos:

Del gráfico anterior, podemos inferir una relación lineal negativa entre los caballos de fuerza y ​​las millas por galón (mpg). Con el aumento de caballos de fuerza, el mpg está disminuyendo.

Ahora, realicemos la regresión lineal simple. 

A partir de la salida del modelo SLR anterior, la ecuación de la línea de mejor ajuste del modelo es 

millas por galón = 39.94 + (-0.16)*(caballos de fuerza)

Al comparar la ecuación anterior con la ecuación del modelo SLR Yi= βiXi + β0 , β0=39.94, β1=-0.16

Ahora, verifique la relevancia del modelo mirando su R² y valores RMSE

R² y los valores RMSE (raíz cuadrática media) son 0.6059 y 4.89, respectivamente. Significa que el 60% de la variación en mpg se explica por la potencia. Para un modelo de regresión lineal simple, este resultado está bien, pero no tanto, ya que podría haber un efecto de otras variables como cilindros, aceleración, etc. El valor RMSE también es muy inferior. 

Veamos cómo la recta se ajusta a los datos.

Del gráfico, podemos inferir que la línea de mejor ajuste puede explicar el efecto de la potencia en mpg.

Regresión lineal múltiple con scikit-learn

Dado que los datos ya están cargados en el sistema, comenzaremos a realizar una regresión lineal múltiple.

Los datos reales tienen 5 variables independientes y 1 variable dependiente (mpg)

La línea de mejor ajuste para la regresión lineal múltiple es 

Y = 46.26 + -0.4 cilindros + -8.313e-05cilindrada + -0.045caballos de fuerza + -0.01peso + -0.03aceleración

Al comparar la ecuación de línea de mejor ajuste con

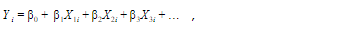
β0 (Intersección)= 46.25, β1 = -0.4, β2 = -8.313e-05, β3= -0.045, β4= 0.01, β5 = -0.03

Ahora, vamos a comprobar la R² y valores RMSE.

R² y los valores RMSE (raíz cuadrática media) son 0.707 y 4.21, respectivamente. Significa que ~71% de la variación en mpg se explica por todos los predictores. Esto representa un buen modelo. Ambos valores son menores que los resultados de la regresión lineal simple, lo que significa que agregar más variables al modelo ayudará a un buen rendimiento del modelo. Sin embargo, cuanto mayor sea el valor de R² y cuanto menor sea el RMSE, mejor será el modelo.

Regresión lineal múltiple: implementación con Python

Tomemos un pequeño conjunto de datos y probemos un modelo de construcción usando python.

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression
from sklearn import metrics

data=pd.read_csv("Consumer.csv")
data.head()

La figura anterior muestra las 5 filas superiores de los datos. En realidad, estamos tratando de predecir la Cantidad cobrada (variable dependiente) con base en las otras dos variables independientes, Ingresos y Tamaño del hogar. Primero verificamos nuestras suposiciones en nuestro conjunto de datos.

1. Comprobar la linealidad

plt.figure(figsize=(14,5))
plt.subplot(1,2,1)
plt.scatter(data['AmountCharged'], data['Income'])
plt.xlabel('AmountCharged')
plt.ylabel('Income')
plt.subplot(1,2,2)
plt.scatter(data['AmountCharged'], data['HouseholdSize'])
plt.xlabel('AmountCharged')
plt.ylabel('HouseholdSize')
plt.show()

Podemos ver en el gráfico anterior que existe una relación lineal entre la cantidad cobrada y los ingresos, el tamaño del hogar.

2. Comprobar la multicolinealidad

sns.scatterplot(data['Income'],data['HouseholdSize'])

No existe colinealidad entre los ingresos y el tamaño del hogar en el gráfico anterior.

Dividimos nuestros datos para entrenar y probar en una proporción de 80:20, respectivamente, usando la función tren_prueba_dividir

X = pd.DataFrame(np.c_[data['Income'], data['HouseholdSize']], columns=['Income','HouseholdSize'])
y=data['AmountCharged']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=9)

3. Comprobar la homocedasticidad

Primero, necesitamos calcular los residuos-

resi=y_test-prediction

Regresión polinomial con scikit-learn

Para la regresión polinomial, usaremos los mismos datos que usamos para la regresión lineal simple. 

El gráfico muestra que la relación entre caballos de fuerza y ​​millas por galón no es perfectamente lineal. Es un poco curvo. 

Gráfico para la línea de mejor ajuste para la regresión lineal simple como se muestra a continuación:

De la gráfica, podemos inferir que la línea de mejor ajuste puede explicar el efecto de la variable independiente, sin embargo, esto no se aplica a la mayoría de los puntos de datos. 

Probemos la regresión polinomial en el conjunto de datos anterior. Ajustemos grado = 2 

Ahora, visualice los resultados de la regresión polinomial

Del gráfico, la línea de mejor ajuste se ve mejor que la Regresión lineal simple. 

Averigüemos el rendimiento del modelo calculando el error absoluto medio, el error cuadrático medio y la raíz cuadrática media.

Rendimiento del modelo de regresión lineal simple:

Regresión polinomial (grado = 2) Rendimiento del modelo:

A partir de los resultados anteriores, podemos ver que los valores de error son menores en la regresión polinomial, pero no hay mucha mejora. Podemos aumentar el grado del polinomio y experimentar con el rendimiento del modelo. 

Regresión lineal avanzada con statsmodels

Hay muchas formas de realizar una regresión en python. 

1. Aprender 
2. modelos estadisticos 

En la MLR en la sección de python explicada anteriormente, hemos realizado MLR utilizando la biblioteca de aprendizaje de scikit. Ahora, realicemos MLR utilizando la biblioteca statsmodels.

Importe las bibliotecas requeridas a continuación

Ahora, realice una regresión lineal múltiple usando statsmodels

De los resultados anteriores, R² y R ajustada² en 0.708 y 0.704, respectivamente. Todas las variables independientes explican casi el 71% de la variación de las variables dependientes. El valor de R² es el mismo que el resultado de la biblioteca de aprendizaje de scikit. 

Al observar el valor de p para las variables independientes, el intercepto, la potencia y el peso son variables importantes ya que el valor de p es inferior a 0.05 (nivel de significación). Podemos intentar realizar MLR eliminando otras variables que no contribuyen al modelo y seleccionando el mejor modelo.

Ahora, verifiquemos el rendimiento del modelo calculando el valor RMSE:

Regresión lineal en R

Contribuido por: Por el Sr. Abhay Poddar

Para ver un ejemplo de regresión lineal en R, elegiremos CARS, que es un conjunto de datos integrado en R. Al escribir CARS en la consola R puede acceder al conjunto de datos. Podemos observar que el conjunto de datos tiene 50 observaciones y 2 variables, a saber, la distancia y la velocidad. El objetivo aquí es predecir la distancia recorrida por un automóvil cuando se conoce la velocidad del automóvil. Además, necesitamos establecer una relación lineal entre ellos con la ayuda de una ecuación aritmética. Antes de adentrarnos en el modelado, siempre es recomendable hacer un Análisis Exploratorio de Datos, que nos ayude a entender los datos y las variables.

Análisis exploratorio de datos

Este documento tiene como objetivo construir un modelo de regresión lineal que pueda ayudar a predecir la distancia. Las siguientes son las visualizaciones básicas que nos ayudarán a entender más sobre los datos y las variables:

1. Diagrama de dispersión: para ayudar a establecer si existe una relación lineal entre la distancia y la velocidad.
2. Diagrama de caja: para verificar si hay valores atípicos en el conjunto de datos.
3. Gráfico de densidad: para verificar la distribución de las variables; idealmente, debería tener una distribución normal.

A continuación se muestran los pasos para hacer estos gráficos en R.

Gráficos de dispersión para visualizar la relación

Un diagrama de dispersión traza los pares de datos numéricos con una variable en cada eje y ayuda a establecer la relación entre las variables independientes y dependientes.

Pasos en R

Si observamos cuidadosamente el diagrama de dispersión, podemos ver que las variables están correlacionadas a medida que caen a lo largo de la línea/curva. Cuanto mayor sea la correlación, más cerca estarán los puntos de la línea/curva. 

Como se discutió anteriormente, el diagrama de dispersión muestra una relación lineal y positiva entre la distancia y la velocidad. Por lo tanto, cumple con uno de los supuestos de la regresión lineal, es decir, debe haber una relación positiva y lineal entre las variables dependientes e independientes.

Verifique los valores atípicos usando diagramas de caja.

Un diagrama de caja también se llama diagrama de caja y bigotes y se usa en estadísticas para representar los resúmenes de cinco números. Se utiliza para verificar si la distribución está sesgada o si hay valores atípicos en el conjunto de datos.

Wikipedia define 'Outliers' como un punto de observación que está distante de otras observaciones en el conjunto de datos.

Ahora, tracemos el Boxplot para buscar valores atípicos.

Después de observar los diagramas de caja para Velocidad y Distancia, podemos decir que no hay valores atípicos en Velocidad, y parece haber un solo valor atípico en Distancia. Por lo tanto, no hay necesidad de tratar los valores atípicos.

Comprobación de la distribución de datos mediante diagramas de densidad

Una de las suposiciones clave para realizar la regresión lineal es que los datos deben distribuirse normalmente. Esto se puede hacer con la ayuda de gráficos de densidad. Un gráfico de densidad nos ayuda a visualizar la distribución de una variable numérica durante un período de tiempo.

Después de observar los diagramas de densidad, podemos concluir que el conjunto de datos tiene una distribución más o menos normal.

Modelado de regresión lineal

Ahora, entremos en la construcción del modelo de regresión lineal. Pero antes de eso, hay una verificación que debemos realizar, que es 'Cálculo de correlación'. Los Coeficientes de Correlación nos ayudan a comprobar qué tan fuerte es la relación entre las variables dependientes e independientes. El valor del Coeficiente de Correlación oscila entre -1 y 1.

Una correlación de 1 indica una relación positiva perfecta. Significa que si el valor de una variable aumenta, el valor de la otra variable también aumenta.

Una correlación de -1 indica una relación negativa perfecta. Significa que si el valor de la variable x aumenta, el valor de la variable y disminuye.

Una Correlación de 0 indica que no hay relación entre las variables.

La salida del Código R anterior es 0.8068949. Muestra que la correlación entre la velocidad y la distancia es de 0.8, que está cerca de 1, lo que indica una correlación positiva y fuerte.

El modelo de regresión lineal en R se construye con la ayuda de la función lm().

La fórmula utiliza dos parámetros principales:

Datos: variable que contiene el conjunto de datos.

Fórmula: un objeto de la clase fórmula.

Los resultados nos muestran el intercepto y el coeficiente beta de la variable velocidad.

De la salida anterior,

a) Podemos escribir la ecuación de regresión como distancia = -17.579 + 3.932 (velocidad).

Diagnóstico del modelo

Solo construir el modelo y usarlo para la predicción es el trabajo a medio hacer. Antes de usar el modelo, debemos asegurarnos de que el modelo sea estadísticamente significativo. Esto significa:

1. Comprobar si existe una relación estadísticamente significativa entre las variables dependientes e independientes.
2. El modelo que construimos se ajusta muy bien a los datos.

Hacemos esto mediante un resumen estadístico del modelo usando la función summary() en R.

El resumen de salida muestra lo siguiente:

1. Llamada: la llamada de función utilizada para calcular el modelo de regresión.
2. Residuos: distribución de residuos, que generalmente tiene una media de 0. Por lo tanto, la mediana no debe estar lejos de 0, y el mínimo y el máximo deben ser iguales en valor absoluto.
3. Coeficientes – Muestra los coeficientes beta de la regresión y su significación estadística.
4. Esfuerzo de soporte residual (RSE), R - Cuadrado y F -Estadística: estas son las métricas para verificar qué tan bien se ajusta el modelo a nuestros datos.

Detección de estadísticas t y valor P

La estadística T y los valores p asociados son métricas muy importantes al verificar el ajuste del modelo.

La estadística t prueba si existe una relación estadísticamente significativa entre las variables independientes y dependientes. Esto significa si el coeficiente beta de la variable independiente es significativamente diferente de 0. Entonces, cuanto mayor sea el valor t, mejor.

Siempre que hay un valor p, siempre hay una hipótesis nula y alternativa asociada con él. El valor p nos ayuda a probar la hipótesis nula, es decir, los coeficientes son iguales a 0. Un valor p bajo significa que podemos rechazar la hipótesis nula.

Las hipótesis estadísticas son las siguientes:

Hipótesis Nula (H0) – Los coeficientes son iguales a cero.

Hipótesis Alternativa (H1) – Los coeficientes no son iguales a cero.

Como se discutió anteriormente, cuando el valor p < 0.05, podemos rechazar con seguridad la hipótesis nula.

En nuestro caso, dado que el valor de p es inferior a 0.05, podemos rechazar la hipótesis nula y concluir que el modelo es altamente significativo. Esto significa que existe una asociación significativa entre las variables independientes y dependientes.

R – Cuadrado y R Ajustado – Cuadrado

R - Squared (R2) es una métrica básica que nos dice cuánta varianza ha sido explicada por el modelo. Va de 0 a 1. En Regresión Lineal, si seguimos agregando nuevas variables, el valor de R – Square seguirá aumentando independientemente de si la variable es significativa. Aquí es donde la R – Cuadrada Ajustada viene a ayudar. El R-cuadrado ajustado nos ayuda a calcular el R-cuadrado solo a partir de aquellas variables cuya adición al modelo es significativa. Por lo tanto, mientras se realiza la regresión lineal, siempre es preferible observar el R-cuadrado ajustado en lugar de solo el R-cuadrado.

1. Un valor de R – Cuadrado ajustado cercano a 1 indica que el modelo de regresión ha explicado una gran proporción de la variabilidad.
2. Un número cercano a 0 indica que el modelo de regresión no explicó demasiada variabilidad.

En nuestra salida, el valor de R cuadrado ajustado es 0.6438, que está más cerca de 1, lo que indica que nuestro modelo ha podido explicar la variabilidad.

AIC y BIC

AIC y BIC son métricas ampliamente utilizadas para la selección de modelos. AIC significa Criterio de información de Akaike y BIC significa Criterio de información bayesiano. Estos nos ayudan a comprobar la bondad de ajuste de nuestro modelo. Para la comparación de modelos, se prefiere el modelo con el AIC y el BIC más bajos.

¿Qué modelo de regresión se ajusta mejor a los datos?

Hay una serie de métricas que nos ayudan a decidir el modelo que mejor se ajusta a nuestros datos, pero las más utilizadas se detallan a continuación:

Estadística	Criterio
R-cuadrado	Cuanto más alto, mejor
R ajustado – al cuadrado	Cuanto más alto, mejor
estadística t	Cuanto más alto sea el valor t, menor será el valor p
estadística f	Cuanto más alto, mejor
AIC	Baja mejor
BIC	Baja mejor
Error estándar medio (MSE)	Baja mejor

Predicción de modelos lineales

Ahora sabemos cómo construir un modelo de regresión lineal en R utilizando el conjunto de datos completo. Pero este enfoque no nos dice qué tan bien funcionará el modelo y qué tan bien se ajustará a los nuevos datos.

Por lo tanto, para resolver este problema, la práctica general en la industria es dividir los datos en conjuntos de datos de Entrenamiento y Prueba en una proporción de 80:20 (Entrenamiento 80% y Prueba 20%). Con la ayuda de este método, ahora podemos obtener los valores del conjunto de datos de prueba y compararlos con los valores del conjunto de datos real.

División de datos

Hacemos esto con la ayuda de la función sample() en R. 

Construyendo el modelo en Train Data y Predict en Test Data

Diagnóstico del modelo

Si nos fijamos en el valor p, dado que es inferior a 0.05, podemos concluir que el modelo es significativo. Además, si comparamos el valor de R – Cuadrado ajustado con el conjunto de datos original, está cerca de él, lo que valida que el modelo es significativo.

K – Validación cruzada de pliegues

Ahora, hemos visto que el modelo también funciona bien en el conjunto de datos de prueba. Pero esto no garantiza que el modelo encaje bien en el futuro también. La razón es que puede darse el caso de que algunos puntos de datos en el conjunto de datos no sean representativos de toda la población. Por lo tanto, necesitamos comprobar el rendimiento del modelo tanto como sea posible. Una forma de garantizar esto es verificar si el modelo funciona bien en fragmentos de datos de entrenamiento y prueba. Esto se puede hacer con la ayuda de K - Validación cruzada de pliegues. 

El procedimiento de K – Validación cruzada de pliegues se proporciona a continuación:

1. La mezcla aleatoria del conjunto de datos.
2. División de datos en k pliegues/secciones/grupos.
3. Para cada pliegue/sección/grupo:

1. Haga el pliegue/sección/grupo de los datos de prueba.
2. Tome el resto de datos como datos del tren.
3. Ejecute el modelo en los datos del tren y evalúe los datos de prueba.
4. Mantenga el puntaje de evaluación y descarte el modelo.

Después de realizar la validación cruzada de K – Fold, podemos observar que el valor de R – Square también está cerca de los datos originales, ya que MAE es del 12 %, lo que nos ayuda a concluir que el modelo se ajusta bien.

Ventajas de usar la regresión lineal

1. El método de regresión lineal es muy fácil de usar. Si se conoce la relación entre las variables (independientes y dependientes), podemos implementar fácilmente el método de regresión en consecuencia (Regresión lineal para relación lineal).
2. La regresión lineal proporciona el nivel de significación de cada atributo que contribuye a la predicción de la variable dependiente. Con estos datos, podemos elegir entre las variables que son variables muy contribuyentes/importantes. 
3. Después de realizar la regresión lineal, obtenemos la línea de mejor ajuste, que se usa en la predicción, que podemos usar de acuerdo con los requisitos comerciales.

Limitaciones de la regresión lineal

La principal limitación de la regresión lineal es que su rendimiento no está a la altura en el caso de una relación no lineal. La regresión lineal puede verse afectada por la presencia de valores atípicos en el conjunto de datos. La presencia de alta correlación entre las variables también conduce al pobre desempeño del modelo de regresión lineal.

Ejemplos de regresión lineal

1. La regresión lineal se puede utilizar para la predicción de ventas de productos para optimizar la gestión del inventario.
2. Se puede utilizar en el dominio de seguros, por ejemplo, para predecir la prima del seguro en función de varias características.
3. El seguimiento diario del número de clics en el sitio web mediante la regresión lineal podría ayudar a optimizar la eficiencia del sitio web, etc.
4. La selección de características es una de las aplicaciones de la regresión lineal.

Regresión lineal: aprendizaje del modelo

• Regresión lineal simple

Con la regresión lineal simple, cuando tenemos una sola entrada, podemos usar estadísticas para estimar los coeficientes.
Esto requiere que calcule las propiedades estadísticas de los datos, como la media, la desviación estándar, la correlación y la covarianza. Todos los datos deben estar disponibles para recorrer y calcular estadísticas.

• Mínimos cuadrados ordinarios

Cuando tenemos más de una entrada, podemos usar Mínimos cuadrados ordinarios para estimar los valores de los coeficientes.
El procedimiento de Mínimos Cuadrados Ordinarios busca minimizar la suma de los cuadrados de los residuos. Esto significa que, dada una línea de regresión a través de los datos, calculamos la distancia desde cada punto de datos hasta la línea de regresión, la elevamos al cuadrado y sumamos todos los errores al cuadrado. Esta es la cantidad que los mínimos cuadrados ordinarios buscan minimizar.

• Descenso de gradiente

Esta operación se llama Descenso de Gradiente y funciona comenzando con valores aleatorios para cada coeficiente. La suma de los errores al cuadrado se calcula para cada par de valores de entrada y salida. Se utiliza una tasa de aprendizaje como factor de escala y los coeficientes se actualizan en la dirección de minimizar el error. El proceso se repite hasta que se logra un error de suma cuadrática mínimo o no es posible ninguna mejora adicional.
Al utilizar este método, debe seleccionar un parámetro de tasa de aprendizaje (alfa) que determina el tamaño del paso de mejora que se debe realizar en cada iteración del procedimiento.

• Regularización

Hay extensiones al entrenamiento del modelo lineal llamadas métodos de regularización. Estos buscan minimizar la suma del error cuadrático del modelo en los datos de entrenamiento (usando mínimos cuadrados ordinarios) y también reducir la complejidad del modelo (como el número o tamaño absoluto de la suma de todos los coeficientes en el modelo).
Dos ejemplos populares de procedimientos de regularización para regresión lineal son:
– Regresión de lazo: donde los Mínimos Cuadrados Ordinarios también se modifican para minimizar la suma absoluta de los coeficientes (llamada regularización L1).
– Regresión de cresta: donde los Mínimos Cuadrados Ordinarios también se modifican para minimizar la suma absoluta al cuadrado de los coeficientes (llamada regularización L2).

Preparación de datos para regresión lineal

La regresión lineal se ha estudiado extensamente y hay mucha literatura sobre cómo se deben estructurar los datos para utilizar mejor el modelo. En la práctica, puede usar estas reglas más como reglas empíricas cuando usa la regresión de mínimos cuadrados ordinarios, la implementación más común de la regresión lineal.

Pruebe diferentes preparaciones de sus datos utilizando estas heurísticas y vea qué funciona mejor para su problema.

• Suposición lineal
• Eliminación de ruido
• Eliminar colinealidad
• Distribuciones gaussianas

Resumen

En esta publicación, descubrió el algoritmo de regresión lineal para el aprendizaje automático.
Cubriste mucho terreno, incluyendo:

• Los nombres comunes utilizados al describir modelos de regresión lineal.
• La representación utilizada por el modelo.
• Los algoritmos de aprendizaje se utilizan para estimar los coeficientes en el modelo.
• Reglas generales a tener en cuenta al preparar datos para su uso con regresión lineal. 

Pruebe la regresión lineal y siéntase cómodo con ella. Si estás planeando una carrera en Aprendizaje automático (Machine learning & LLM), aquí están algunas Imprescindibles en tu currículum y del preguntas de entrevista mas comunes preparar.

• Distribución de relaciones públicas y contenido potenciado por SEO. Consiga amplificado hoy.
• Platoblockchain. Inteligencia del Metaverso Web3. Conocimiento amplificado. Accede Aquí.
• Fuente: https://www.mygreatlearning.com/blog/linear-regression-in-machine-learning/