Imagen por editor
 

Como dijo una vez Karl Pearson, un matemático británico, Estadística es la gramática de la ciencia y esto se aplica especialmente a las ciencias informáticas y de la información, las ciencias físicas y las ciencias biológicas. Cuando usted está comenzando con su viaje en Data science or Data Analytics, tener conocimientos estadísticos lo ayudará a aprovechar mejor los conocimientos de los datos.

“La estadística es la gramática de la ciencia”. carl pearson

La importancia de las estadísticas en la ciencia de datos y el análisis de datos no se puede subestimar. Las estadísticas proporcionan herramientas y métodos para encontrar la estructura y brindar información más profunda sobre los datos. Tanto la Estadística como las Matemáticas aman los hechos y odian las conjeturas. Conocer los fundamentos de estos dos temas importantes le permitirá pensar críticamente y ser creativo al usar los datos para resolver problemas comerciales y tomar decisiones basadas en datos. En este artículo, cubriré los siguientes temas de estadísticas para la ciencia de datos y el análisis de datos:

- Random variables - Probability distribution functions (PDFs) - Mean, Variance, Standard Deviation - Covariance and Correlation - Bayes Theorem - Linear Regression and Ordinary Least Squares (OLS) - Gauss-Markov Theorem - Parameter properties (Bias, Consistency, Efficiency) - Confidence intervals - Hypothesis testing - Statistical significance - Type I & Type II Errors - Statistical tests (Student's t-test, F-test) - p-value and its limitations - Inferential Statistics - Central Limit Theorem & Law of Large Numbers - Dimensionality reduction techniques (PCA, FA)

Si no tiene conocimientos estadísticos previos y desea identificar y aprender los conceptos estadísticos esenciales desde cero, para prepararse para sus entrevistas de trabajo, este artículo es para usted. Este artículo también será una buena lectura para cualquiera que quiera refrescar sus conocimientos estadísticos.

Bienvenido a LunarTech.ai, donde entendemos el poder de las estrategias de búsqueda de empleo en el dinámico campo de la ciencia de datos y la IA. Profundizamos en las tácticas y estrategias necesarias para navegar el competitivo proceso de búsqueda de empleo. Ya sea que defina sus objetivos profesionales, personalice los materiales de solicitud o aproveche las bolsas de trabajo y las redes, nuestros conocimientos le brindan la orientación que necesita para conseguir el trabajo de sus sueños.

¿Preparándose para entrevistas de ciencia de datos? ¡No temáis! Iluminamos las complejidades del proceso de la entrevista, brindándole el conocimiento y la preparación necesarios para aumentar sus posibilidades de éxito. Desde las evaluaciones telefónicas iniciales hasta las evaluaciones técnicas, las entrevistas técnicas y las entrevistas de comportamiento, no dejamos piedra sin remover.

At LunarTech.ai, vamos más allá de la teoría. Somos su trampolín hacia el éxito sin precedentes en el ámbito de la tecnología y la ciencia de datos. Nuestro viaje de aprendizaje integral está diseñado para adaptarse perfectamente a su estilo de vida, lo que le permite lograr el equilibrio perfecto entre los compromisos personales y profesionales mientras adquiere habilidades de vanguardia. Con nuestra dedicación al crecimiento de su carrera, incluida la asistencia para la colocación laboral, la creación de un currículum vitae experto y la preparación de entrevistas, emergerá como una potencia lista para la industria.

Únase a nuestra comunidad de personas ambiciosas hoy y emprendan juntos este emocionante viaje de ciencia de datos. Con LunarTech.ai, el futuro es brillante y usted tiene las llaves para desbloquear oportunidades ilimitadas.

El concepto de variables aleatorias constituye la piedra angular de muchos conceptos estadísticos. Puede ser difícil de digerir su definición matemática formal, pero en pocas palabras, un variable aleatoria es una forma de asignar los resultados de procesos aleatorios, como lanzar una moneda o tirar un dado, a números. Por ejemplo, podemos definir el proceso aleatorio de lanzar una moneda por la variable aleatoria X que toma el valor 1 si el resultado si ¡Aviso! y 0 si el resultado es cruz.

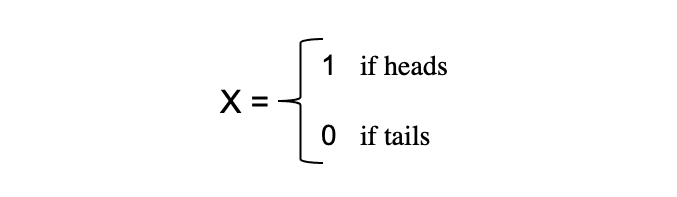
En este ejemplo, tenemos un proceso aleatorio de lanzar una moneda donde este experimento puede producir dos posibles resultados: {0,1}. Este conjunto de todos los resultados posibles se llama espacio muestral del experimento Cada vez que se repite el proceso aleatorio, se denomina evento. En este ejemplo, lanzar una moneda al aire y obtener cruz como resultado es un evento. La oportunidad o la probabilidad de que ocurra este evento con un resultado particular se denomina probabilidades de ese evento. Una probabilidad de un evento es la posibilidad de que una variable aleatoria tome un valor específico de x que puede ser descrito por P(x). En el ejemplo de lanzar una moneda, la probabilidad de obtener cara o cruz es la misma, es decir, 0.5 o 50 %. Entonces tenemos la siguiente configuración:

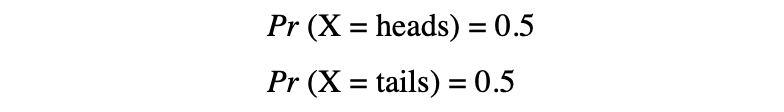
donde la probabilidad de un evento, en este ejemplo, solo puede tomar valores en el rango [0,1].

La importancia de las estadísticas en la ciencia de datos y el análisis de datos no se puede subestimar. Las estadísticas proporcionan herramientas y métodos para encontrar la estructura y brindar información más profunda sobre los datos.

Para comprender los conceptos de media, varianza y muchos otros temas estadísticos, es importante aprender los conceptos de población y muestra. El población es el conjunto de todas las observaciones (individuos, objetos, eventos o procedimientos) y suele ser muy grande y diverso, mientras que un muestra es un subconjunto de observaciones de la población que idealmente es una verdadera representación de la población.

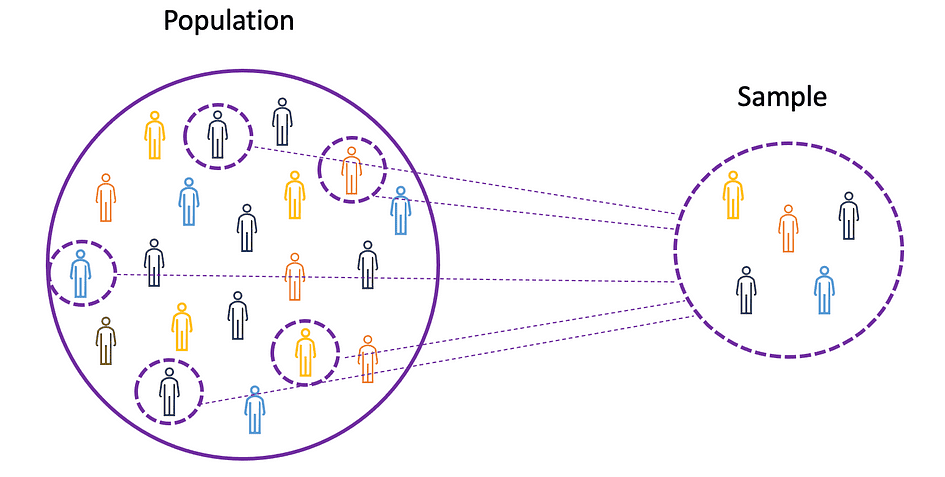
Fuente de la imagen: El autor

Dado que experimentar con una población completa es imposible o simplemente demasiado costoso, los investigadores o analistas usan muestras en lugar de la población completa en sus experimentos o ensayos. Para asegurarse de que los resultados experimentales sean confiables y válidos para toda la población, la muestra debe ser una representación real de la población. Es decir, la muestra debe ser imparcial. Para este propósito, se pueden utilizar técnicas de muestreo estadístico tales como Muestreo aleatorio, muestreo sistemático, muestreo por conglomerados, muestreo ponderado y muestreo estratificado.

Media

La media, también conocida como promedio, es un valor central de un conjunto finito de números. Supongamos que una variable aleatoria X en los datos tiene los siguientes valores:

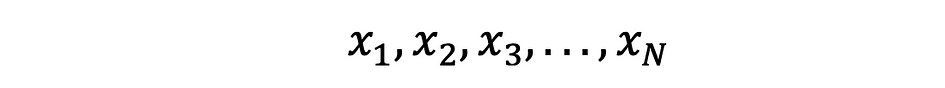
donde N es el número de observaciones o puntos de datos en el conjunto de muestras o simplemente la frecuencia de los datos. Entonces el muestra promedio definido por ?, que se utiliza muy a menudo para aproximar la media poblacional, se puede expresar de la siguiente manera:

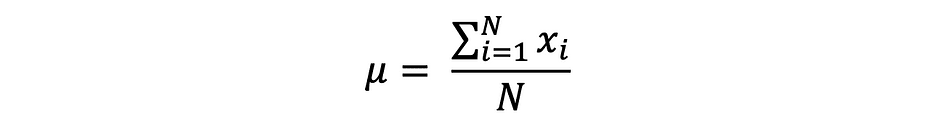
La media también se conoce como expectativa que a menudo se define por E() o variable aleatoria con una barra en la parte superior. Por ejemplo, la expectativa de las variables aleatorias X e Y, es decir E(X) y E(Y), respectivamente, se puede expresar de la siguiente manera:

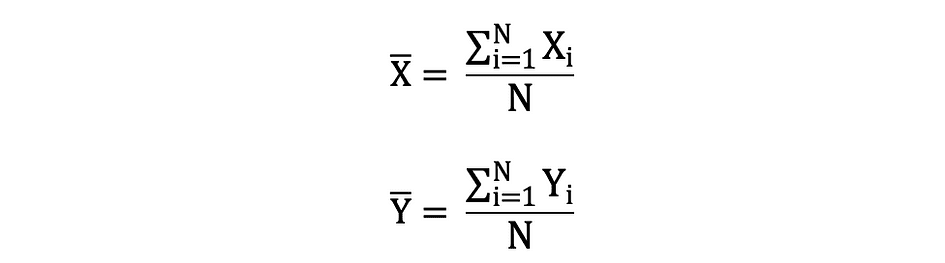
import numpy as np
import math
x = np.array([1,3,5,6])
mean_x = np.mean(x)
# in case the data contains Nan values
x_nan = np.array([1,3,5,6, math.nan])
mean_x_nan = np.nanmean(x_nan)

Diferencia

La varianza mide la distancia entre los puntos de datos y el valor promedio, y es igual a la suma de los cuadrados de las diferencias entre los valores de los datos y el promedio (la media). Además, el varianza poblacional, se puede expresar de la siguiente manera:

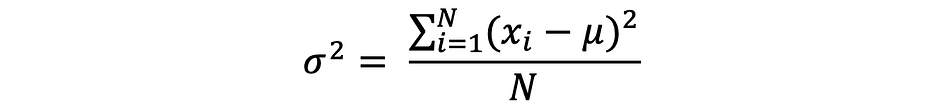
x = np.array([1,3,5,6])
variance_x = np.var(x) # here you need to specify the degrees of freedom (df) max number of logically independent data points that have freedom to vary
x_nan = np.array([1,3,5,6, math.nan])
mean_x_nan = np.nanvar(x_nan, ddof = 1)

Para derivar expectativas y varianzas de diferentes funciones populares de distribución de probabilidad, echa un vistazo a este repositorio de Github.

Desviación Estándar

La desviación estándar es simplemente la raíz cuadrada de la varianza y mide la medida en que los datos varían de su media. La desviación estándar definida por sigma se puede expresar de la siguiente manera:

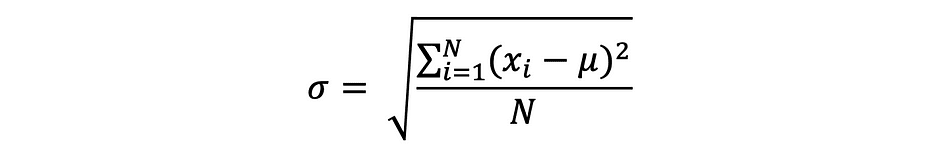
A menudo se prefiere la desviación estándar a la varianza porque tiene la misma unidad que los puntos de datos, lo que significa que puede interpretarla más fácilmente.

x = np.array([1,3,5,6])
variance_x = np.std(x) x_nan = np.array([1,3,5,6, math.nan])
mean_x_nan = np.nanstd(x_nan, ddof = 1)

Covarianza

La covarianza es una medida de la variabilidad conjunta de dos variables aleatorias y describe la relación entre estas dos variables. Se define como el valor esperado del producto de las desviaciones de las medias de dos variables aleatorias. La covarianza entre dos variables aleatorias X y Z se puede describir mediante la siguiente expresión, donde E(X) y E(Z) representan las medias de X y Z, respectivamente.

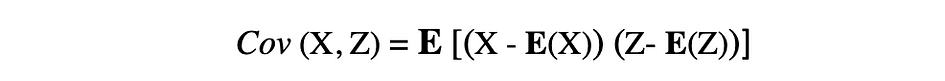
La covarianza puede tomar valores negativos o positivos, así como el valor 0. Un valor positivo de la covarianza indica que dos variables aleatorias tienden a variar en la misma dirección, mientras que un valor negativo sugiere que estas variables varían en direcciones opuestas. Finalmente, el valor 0 significa que no varían entre sí.

x = np.array([1,3,5,6])
y = np.array([-2,-4,-5,-6])
#this will return the covariance matrix of x,y containing x_variance, y_variance on diagonal elements and covariance of x,y
cov_xy = np.cov(x,y)

La correlación

La correlación también es una medida de relación y mide tanto la fuerza como la dirección de la relación lineal entre dos variables. Si se detecta una correlación, significa que existe una relación o un patrón entre los valores de dos variables objetivo. La correlación entre dos variables aleatorias X y Z es igual a la covarianza entre estas dos variables dividida por el producto de las desviaciones estándar de estas variables, que se puede describir mediante la siguiente expresión.

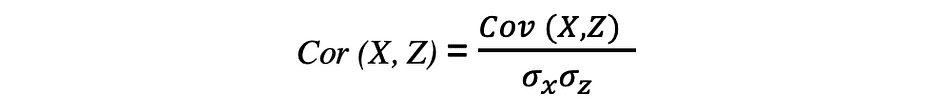
Los valores de los coeficientes de correlación oscilan entre -1 y 1. Tenga en cuenta que la correlación de una variable consigo misma es siempre 1, es decir Co(X, X) = 1. Otra cosa a tener en cuenta al interpretar la correlación es no confundirla con causalidad, dado que una correlación no es causalidad. Incluso si hay una correlación entre dos variables, no puede concluir que una variable provoca un cambio en la otra. Esta relación podría ser una coincidencia, o un tercer factor podría estar causando que ambas variables cambien.

x = np.array([1,3,5,6])
y = np.array([-2,-4,-5,-6])
corr = np.corrcoef(x,y)

Una función que describe todos los valores posibles, el espacio muestral y las probabilidades correspondientes que puede tomar una variable aleatoria dentro de un rango dado, acotado entre los valores mínimo y máximo posibles, se llama una función de distribución de probabilidad (pdf) o densidad de probabilidad. Cada pdf debe satisfacer los siguientes dos criterios:

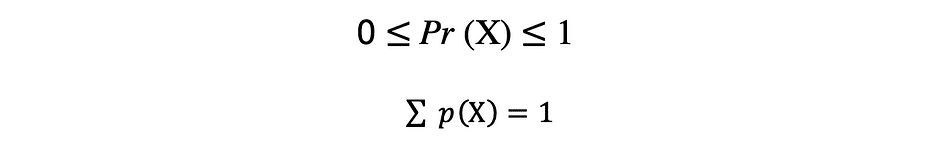
donde el primer criterio establece que todas las probabilidades deben ser números en el rango de [0,1] y el segundo criterio establece que la suma de todas las probabilidades posibles debe ser igual a 1.

Las funciones de probabilidad generalmente se clasifican en dos categorías: discreto y continuo. Discreto   La función describe el proceso aleatorio con contable espacio muestral, como en el caso de un ejemplo de lanzar una moneda que tiene solo dos resultados posibles. Continuo La función de distribución describe el proceso aleatorio con continuo espacio muestral. Ejemplos de funciones de distribución discretas son bernoulli, Binomio, Poisson, Uniforme discreto. Ejemplos de funciones de distribución continua son NORMAL, uniforme continuo, Cauchy.

Distribución binomial

La distribución binomial es la distribución de probabilidad discreta del número de éxitos en una secuencia de n experimentos independientes, cada uno con el resultado de valor booleano: comercial (con probabilidad p) o el fracaso (con probabilidad q = 1? pag). Supongamos que una variable aleatoria X sigue una distribución Binomial, entonces la probabilidad de observar k los éxitos en n ensayos independientes se pueden expresar mediante la siguiente función de densidad de probabilidad:

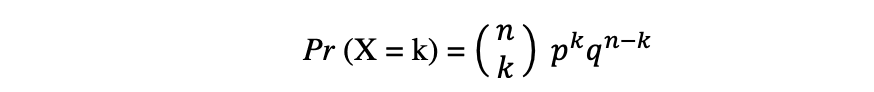
La distribución binomial es útil cuando se analizan los resultados de experimentos independientes repetidos, especialmente si uno está interesado en la probabilidad de alcanzar un umbral particular dada una tasa de error específica.

Media y varianza de distribución binomial

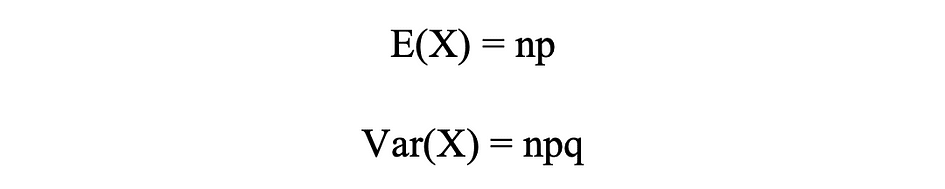
La siguiente figura visualiza un ejemplo de distribución Binomial donde el número de ensayos independientes es igual a 8 y la probabilidad de éxito en cada ensayo es igual al 16%.

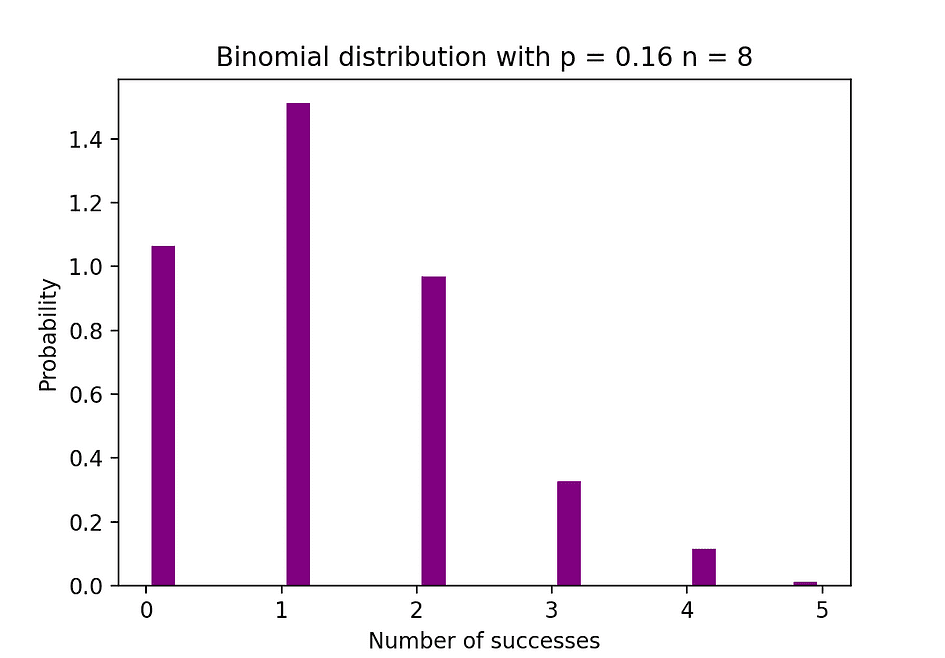
Fuente de la imagen: El autor

# Random Generation of 1000 independent Binomial samples
import numpy as np
n = 8
p = 0.16
N = 1000
X = np.random.binomial(n,p,N)
# Histogram of Binomial distribution
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 20, density = True, rwidth = 0.7, color = 'purple')
plt.title("Binomial distribution with p = 0.16 n = 8")
plt.xlabel("Number of successes")
plt.ylabel("Probability")
plt.show()

Distribución de veneno

La distribución de Poisson es la distribución de probabilidad discreta del número de eventos que ocurren en un período de tiempo específico, dado el número promedio de veces que ocurre el evento durante ese período de tiempo. Supongamos que una variable aleatoria X sigue una distribución de Poisson, entonces la probabilidad de observar k Los eventos durante un período de tiempo se pueden expresar mediante la siguiente función de probabilidad:

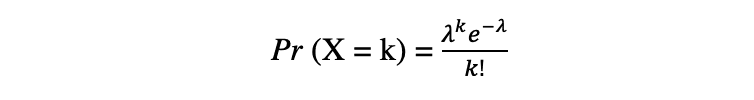
donde e is Número de Euler y ? lambda, la parámetro de tasa de llegada is el valor esperado de X. La función de distribución de Poisson es muy popular por su uso en el modelado de eventos contables que ocurren dentro de un intervalo de tiempo determinado.

Media y varianza de distribución de Poisson

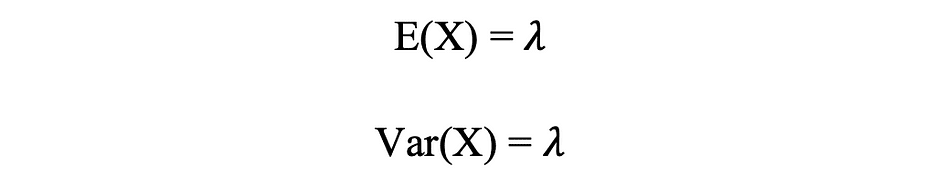
Por ejemplo, la distribución de Poisson se puede utilizar para modelar la cantidad de clientes que llegan a la tienda entre las 7 y las 10 p. m., o la cantidad de pacientes que llegan a una sala de emergencias entre las 11 y las 12 p. m. La siguiente figura visualiza un ejemplo de distribución de Poisson donde contamos el número de visitantes de la web que llegan al sitio web donde se supone que la tasa de llegada, lambda, es igual a 7 minutos.

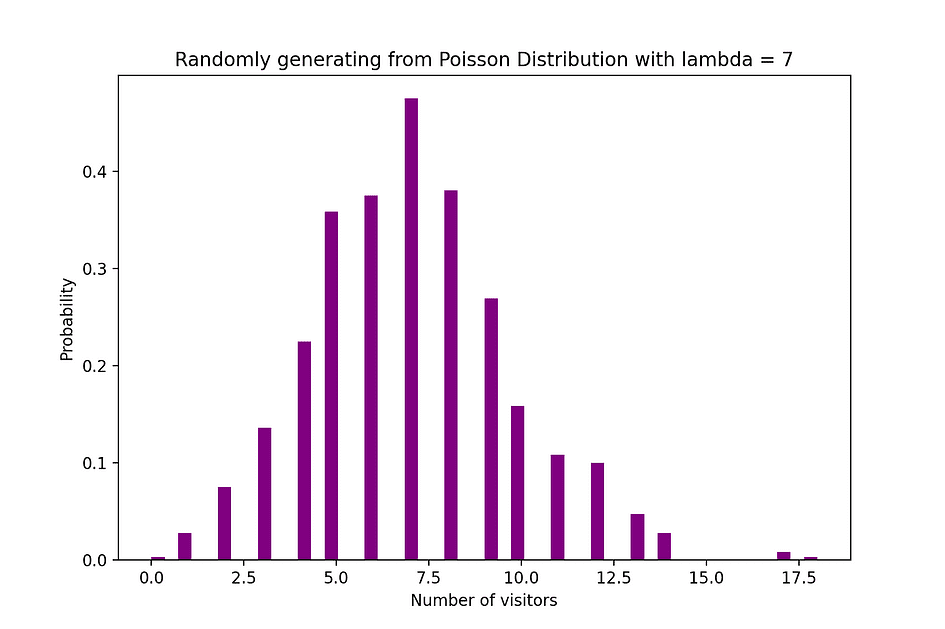
Fuente de la imagen: El autor

# Random Generation of 1000 independent Poisson samples
import numpy as np
lambda_ = 7
N = 1000
X = np.random.poisson(lambda_,N) # Histogram of Poisson distribution
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 50, density = True, color = 'purple')
plt.title("Randomly generating from Poisson Distribution with lambda = 7")
plt.xlabel("Number of visitors")
plt.ylabel("Probability")
plt.show()

Distribución normal

La distribución de probabilidad Normal es la distribución de probabilidad continua para una variable aleatoria de valor real. Distribución normal, también llamada distribución gaussiana es posiblemente una de las funciones de distribución más populares que se usan comúnmente en las ciencias sociales y naturales para fines de modelado, por ejemplo, se usa para modelar la altura de las personas o los puntajes de las pruebas. Supongamos que una variable aleatoria X sigue una distribución Normal, entonces su función de densidad de probabilidad se puede expresar de la siguiente manera.

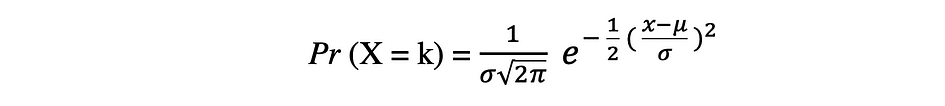
donde el parámetro ? (mu) es la media de la distribución también conocida como la parámetro de ubicación, parámetro ? (sigma) es la desviación estándar de la distribución también conocida como la parámetro de escala. El número ? (pi) es una constante matemática aproximadamente igual a 3.14.

Distribución normal media y varianza

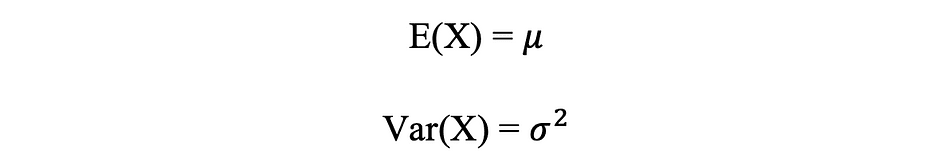
La siguiente figura visualiza un ejemplo de distribución Normal con media 0 (? = 0) y desviación estándar de 1 (? = 1), que se denomina Normal normal distribución que es simétrico.

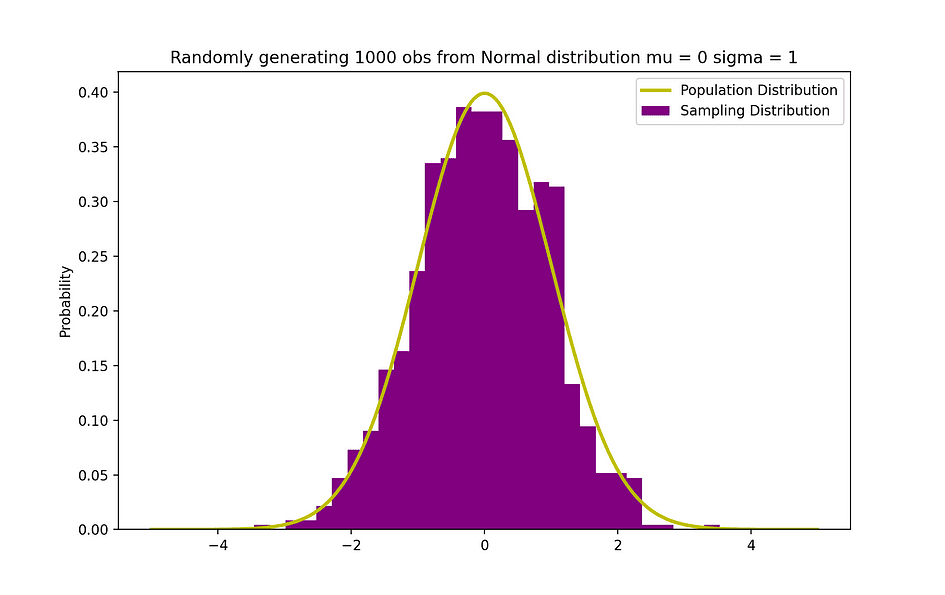
Fuente de la imagen: El autor

# Random Generation of 1000 independent Normal samples
import numpy as np
mu = 0
sigma = 1
N = 1000
X = np.random.normal(mu,sigma,N) # Population distribution
from scipy.stats import norm
x_values = np.arange(-5,5,0.01)
y_values = norm.pdf(x_values)
#Sample histogram with Population distribution
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 30, density = True,color = 'purple',label = 'Sampling Distribution')
plt.plot(x_values,y_values, color = 'y',linewidth = 2.5,label = 'Population Distribution')
plt.title("Randomly generating 1000 obs from Normal distribution mu = 0 sigma = 1")
plt.ylabel("Probability")
plt.legend()
plt.show()

El Teorema de Bayes o a menudo llamado Ley de Bayes es posiblemente la regla más poderosa de probabilidad y estadística, llamada así por el famoso estadístico y filósofo inglés Thomas Bayes.

Fuente de imagen: Wikipedia

El teorema de Bayes es una poderosa ley de probabilidad que trae el concepto de subjetividad al mundo de la Estadística y las Matemáticas donde todo se trata de hechos. Describe la probabilidad de un evento, con base en la información previa de condiciones que podría estar relacionado con ese evento. Por ejemplo, si se sabe que el riesgo de contraer coronavirus o covid-19 aumenta con la edad, entonces el teorema de Bayes permite que el riesgo para un individuo de una edad conocida se determine con mayor precisión condicionándolo a la edad que simplemente asumiendo que este individuo es común a la población en su conjunto.

El concepto de la probabilidad condicional, que juega un papel central en la teoría de Bayes, es una medida de la probabilidad de que suceda un evento, dado que ya ha ocurrido otro evento. El teorema de Bayes se puede describir mediante la siguiente expresión, donde X e Y representan los eventos X e Y, respectivamente:

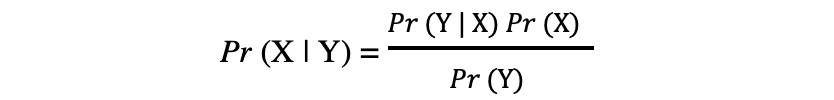
• Pr (X|Y): la probabilidad de que ocurra el evento X dado que el evento o la condición Y ha ocurrido o es cierto
• Pr (Y|X): la probabilidad de que ocurra el evento Y dado que el evento o la condición X ha ocurrido o es cierto
• Pr (X) & Pr (Y): las probabilidades de observar los eventos X e Y, respectivamente

En el caso del ejemplo anterior, la probabilidad de contraer Coronavirus (evento X) condicionada a tener una edad determinada es Pr (X|Y), que es igual a la probabilidad de tener una cierta edad dado que uno tiene Coronavirus, Pr (Y|X), multiplicado por la probabilidad de contraer un Coronavirus, Pr (X), dividida entre la probabilidad de tener cierta edad., Pr (Y).

Anteriormente se introdujo el concepto de causalidad entre variables, que ocurre cuando una variable tiene un impacto directo sobre otra variable. Cuando la relación entre dos variables es lineal, la regresión lineal es un método estadístico que puede ayudar a modelar el impacto de un cambio de unidad en una variable. las variable independiente en los valores de otra variable, la variable dependiente.

Las variables dependientes a menudo se denominan variables de respuesta or explicado las variables, mientras que las variables independientes a menudo se denominan regresores or variables explicativas. Cuando el modelo de regresión lineal se basa en una sola variable independiente, el modelo se llama Regresión lineal simple y cuando el modelo se basa en múltiples variables independientes, se denomina Regresión lineal múltiple. La regresión lineal simple se puede describir mediante la siguiente expresión:

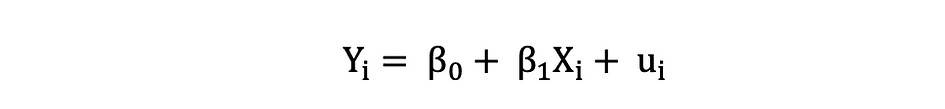
donde Y es la variable dependiente, X es la variable independiente que forma parte de los datos, ?0 es el intercepto que es desconocido y constante, ?1 es el coeficiente de la pendiente o un parámetro correspondiente a la variable X que también es desconocida y constante. Finalmente, u es el término de error que comete el modelo al estimar los valores de Y. La idea principal detrás de la regresión lineal es encontrar la línea recta que mejor se ajuste, la línea de regresión, a través de un conjunto de datos emparejados (X, Y). Un ejemplo de la aplicación de regresión lineal es modelar el impacto de Longitud de la aleta en los pingüinos Masa corporal, que se visualiza a continuación.

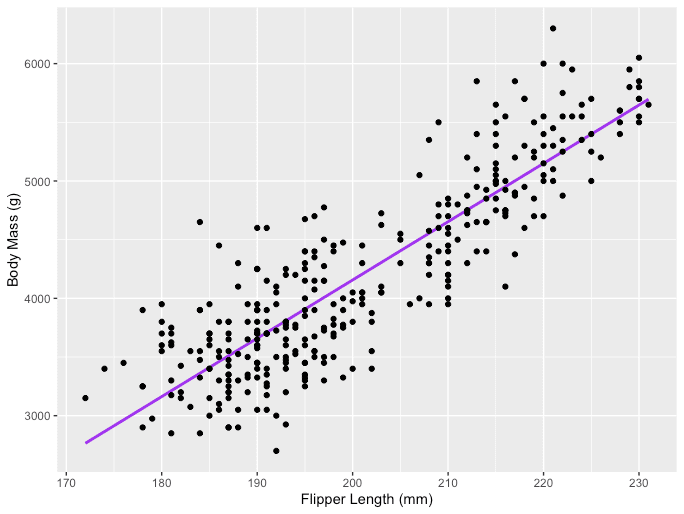
Fuente de la imagen: El autor

# R code for the graph
install.packages("ggplot2")
install.packages("palmerpenguins")
library(palmerpenguins)
library(ggplot2)
View(data(penguins))
ggplot(data = penguins, aes(x = flipper_length_mm,y = body_mass_g))+ geom_smooth(method = "lm", se = FALSE, color = 'purple')+ geom_point()+ labs(x="Flipper Length (mm)",y="Body Mass (g)")

La regresión lineal múltiple con tres variables independientes se puede describir mediante la siguiente expresión:

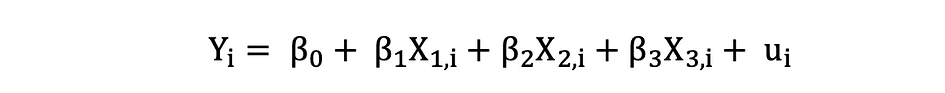
Mínimos cuadrados ordinarios

Los mínimos cuadrados ordinarios (OLS) es un método para estimar los parámetros desconocidos como ?0 y ?1 en un modelo de regresión lineal. El modelo se basa en el principio de mínimos cuadrados esa minimiza la suma de los cuadrados de las diferencias entre la variable dependiente observada y sus valores predichos por la función lineal de la variable independiente, a menudo denominada valores ajustados. Esta diferencia entre los valores real y predicho de la variable dependiente Y se conoce como residual y lo que hace OLS es minimizar la suma de los residuos al cuadrado. Este problema de optimización da como resultado las siguientes estimaciones de MCO para los parámetros desconocidos ?0 y ?1, que también se conocen como estimaciones de coeficientes.

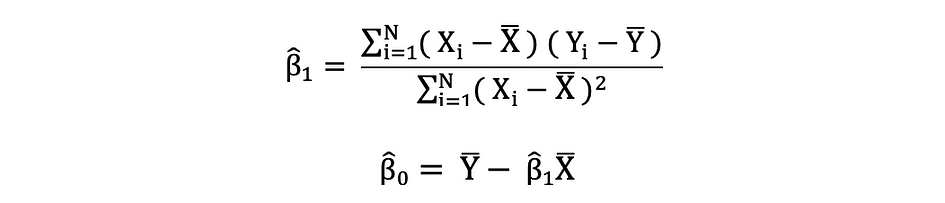
Una vez estimados estos parámetros del modelo de Regresión Lineal Simple, el valores ajustados de la variable de respuesta se puede calcular de la siguiente manera:

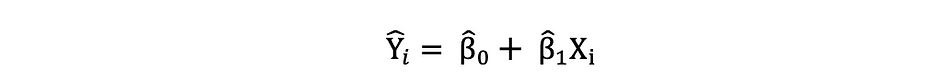
Error estándar

El derechos residuales de autor o los términos de error estimados se pueden determinar de la siguiente manera:

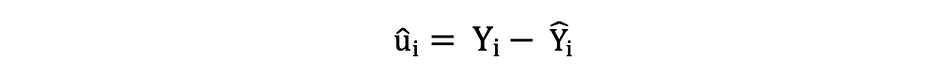
Es importante tener en cuenta la diferencia entre los términos de error y los residuos. Los términos de error nunca se observan, mientras que los residuos se calculan a partir de los datos. El OLS estima los términos de error para cada observación, pero no el término de error real. Por lo tanto, la varianza del error real aún se desconoce. Además, estas estimaciones están sujetas a la incertidumbre del muestreo. Lo que esto significa es que nunca podremos determinar la estimación exacta, el valor real, de estos parámetros a partir de datos de muestra en una aplicación empírica. Sin embargo, podemos estimarlo calculando el muestra varianza residual utilizando los residuos de la siguiente manera.

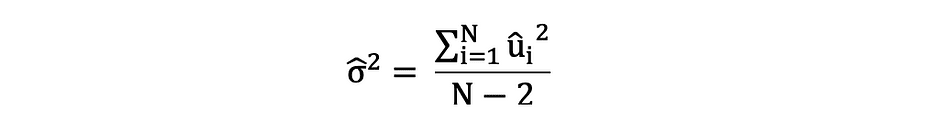
Esta estimación de la varianza de los residuos de la muestra ayuda a estimar la varianza de los parámetros estimados, que a menudo se expresa de la siguiente manera:

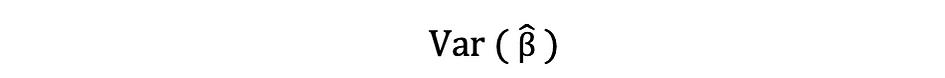
La raíz cuadrada de este término de varianza se llama el error estándar de la estimación, que es un componente clave para evaluar la precisión de las estimaciones de los parámetros. Se utiliza para calcular estadísticas de prueba e intervalos de confianza. El error estándar se puede expresar de la siguiente manera:

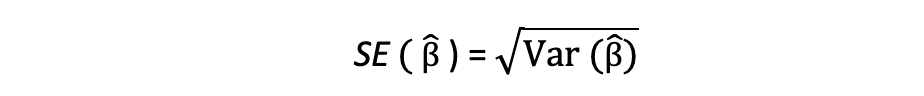
Es importante tener en cuenta la diferencia entre los términos de error y los residuos. Los términos de error nunca se observan, mientras que los residuos se calculan a partir de los datos.

Supuestos de MCO

El método de estimación OLS hace la siguiente suposición que debe cumplirse para obtener resultados de predicción confiables:

A1: Linealidad La suposición establece que el modelo es lineal en los parámetros.

A2: Aleatorio Muestra La suposición establece que todas las observaciones en la muestra se seleccionan al azar.

A3: exogeneidad La suposición establece que las variables independientes no están correlacionadas con los términos de error.

A4: Homocedasticidad La suposición establece que la varianza de todos los términos de error es constante.

A5: Sin multicolinealidad perfecta La suposición establece que ninguna de las variables independientes es constante y que no existen relaciones lineales exactas entre las variables independientes.

def runOLS(Y,X): # OLS esyimation Y = Xb + e --> beta_hat = (X'X)^-1(X'Y) beta_hat = np.dot(np.linalg.inv(np.dot(np.transpose(X), X)), np.dot(np.transpose(X), Y)) # OLS prediction Y_hat = np.dot(X,beta_hat) residuals = Y-Y_hat RSS = np.sum(np.square(residuals)) sigma_squared_hat = RSS/(N-2) TSS = np.sum(np.square(Y-np.repeat(Y.mean(),len(Y)))) MSE = sigma_squared_hat RMSE = np.sqrt(MSE) R_squared = (TSS-RSS)/TSS # Standard error of estimates:square root of estimate's variance var_beta_hat = np.linalg.inv(np.dot(np.transpose(X),X))*sigma_squared_hat SE = [] t_stats = [] p_values = [] CI_s = [] for i in range(len(beta)): #standard errors SE_i = np.sqrt(var_beta_hat[i,i]) SE.append(np.round(SE_i,3)) #t-statistics t_stat = np.round(beta_hat[i,0]/SE_i,3) t_stats.append(t_stat) #p-value of t-stat p[|t_stat| >= t-treshhold two sided] p_value = t.sf(np.abs(t_stat),N-2) * 2 p_values.append(np.round(p_value,3)) #Confidence intervals = beta_hat -+ margin_of_error t_critical = t.ppf(q =1-0.05/2, df = N-2) margin_of_error = t_critical*SE_i CI = [np.round(beta_hat[i,0]-margin_of_error,3), np.round(beta_hat[i,0]+margin_of_error,3)] CI_s.append(CI) return(beta_hat, SE, t_stats, p_values,CI_s, MSE, RMSE, R_squared)

Bajo el supuesto de que se satisfacen los criterios de MCO A1 — A5, los estimadores de MCO de los coeficientes β0 y β1 son AZUL y Consistente.

Teorema de Gauss-Markov

Este teorema destaca las propiedades de las estimaciones de OLS donde el término AZUL representa Mejor estimador lineal imparcial.

Parcialidad

El parcialidad de un estimador es la diferencia entre su valor esperado y el valor real del parámetro que se está estimando y se puede expresar de la siguiente manera:

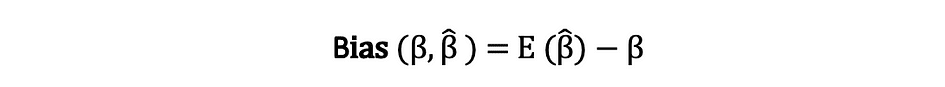
Cuando decimos que el estimador es imparcial lo que queremos decir es que el sesgo es igual a cero, lo que implica que el valor esperado del estimador es igual al valor verdadero del parámetro, es decir:

La falta de sesgo no garantiza que la estimación obtenida con una muestra en particular sea igual o cercana a ?. Lo que significa es que, si uno repetidamente extrae muestras aleatorias de la población y luego calcula la estimación cada vez, entonces el promedio de estas estimaciones sería igual o muy cercano a β.

Eficiencia

El término Best en el teorema de Gauss-Markov se relaciona con la varianza del estimador y se denomina eficiencia. Un parámetro puede tener varios estimadores, pero el que tiene la varianza más baja se llama eficiente.

Consistencia

El término consistencia va de la mano con los términos tamaño de la muestra y convergencia. Si el estimador converge al parámetro verdadero a medida que el tamaño de la muestra se vuelve muy grande, entonces se dice que este estimador es consistente, es decir:

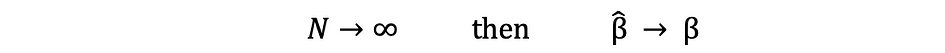
Bajo el supuesto de que se satisfacen los criterios de MCO A1 — A5, los estimadores de MCO de los coeficientes β0 y β1 son AZUL y Consistente.
Teorema de Gauss-Markov

Todas estas propiedades son válidas para las estimaciones de MCO como se resume en el teorema de Gauss-Markov. En otras palabras, las estimaciones de OLS tienen la varianza más pequeña, son imparciales, lineales en los parámetros y consistentes. Estas propiedades se pueden probar matemáticamente utilizando las suposiciones de MCO hechas anteriormente.

El Intervalo de Confianza es el rango que contiene el verdadero parámetro de la población con una cierta probabilidad pre-especificada, referido como el nivel de confianza del experimento, y se obtiene utilizando los resultados de la muestra y el margen de error.

Margen de error

El margen de error es la diferencia entre los resultados de la muestra y en función de cuál habría sido el resultado si se hubiera utilizado toda la población.

Nivel de confianza

El Nivel de Confianza describe el nivel de certeza en los resultados experimentales. Por ejemplo, un nivel de confianza del 95% significa que si uno fuera a realizar el mismo experimento repetidamente 100 veces, entonces 95 de esos 100 ensayos conducirían a resultados similares. Tenga en cuenta que el nivel de confianza se define antes del inicio del experimento porque afectará el tamaño del margen de error al final del experimento.

Intervalo de confianza para estimaciones OLS

Como se mencionó anteriormente, las estimaciones de OLS de la Regresión Lineal Simple, las estimaciones para el intercepto ?0 y el coeficiente de pendiente ?1, están sujetas a la incertidumbre de muestreo. Sin embargo, podemos construir CI para estos parámetros que contendrá el valor real de estos parámetros en el 95% de todas las muestras. Es decir, intervalo de confianza del 95% para ? puede interpretarse de la siguiente manera:

• El intervalo de confianza es el conjunto de valores para los cuales no se puede rechazar una prueba de hipótesis al nivel del 5%.
• El intervalo de confianza tiene un 95 % de posibilidades de contener el verdadero valor de ?.

El intervalo de confianza del 95% de las estimaciones de OLS se puede construir de la siguiente manera:

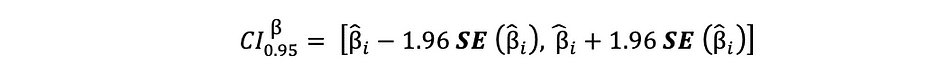
que se basa en la estimación del parámetro, el error estándar de esa estimación y el valor 1.96 que representa el margen de error correspondiente a la regla de rechazo del 5%. Este valor se determina utilizando el Tabla de distribución normal, que se discutirá más adelante en este artículo. Mientras tanto, la siguiente figura ilustra la idea del IC del 95%:

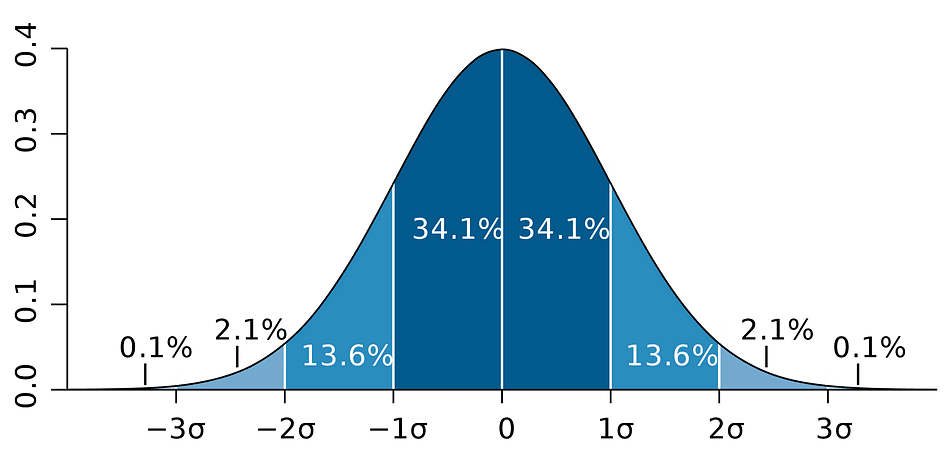
Fuente de imagen: Wikipedia

Tenga en cuenta que el intervalo de confianza también depende del tamaño de la muestra, dado que se calcula utilizando el error estándar que se basa en el tamaño de la muestra.

El nivel de confianza se define antes del inicio del experimento porque afectará el tamaño del margen de error al final del experimento.

Probar una hipótesis en Estadística es una forma de probar los resultados de un experimento o encuesta para determinar qué tan significativos son los resultados. Básicamente, uno está probando si los resultados obtenidos son válidos calculando las probabilidades de que los resultados hayan ocurrido por casualidad. Si es la letra, entonces los resultados no son fiables y tampoco lo es el experimento. La prueba de hipótesis es parte del Inferencia estadística.

Hipótesis nula y alternativa

En primer lugar, debe determinar la tesis que desea probar, luego debe formular la Hipótesis nula y del Hipótesis alternativa. La prueba puede tener dos resultados posibles y, en función de los resultados estadísticos, puede rechazar la hipótesis establecida o aceptarla. Como regla general, los estadísticos tienden a poner la versión o formulación de la hipótesis bajo la Hipótesis Nula de que eso hay que rechazarlo, mientras que la versión aceptable y deseada se establece bajo la Hipótesis Alternativa.

Significancia estadística

Veamos el ejemplo mencionado anteriormente en el que se usó el modelo de regresión lineal para investigar si un pingüino Longitud de la aleta, la variable independiente, tiene un impacto en Masa corporal, la variable dependiente. Podemos formular este modelo con la siguiente expresión estadística:

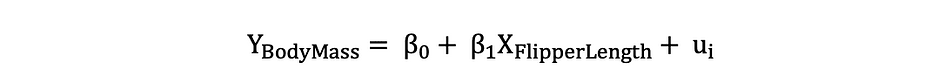
Luego, una vez que se estiman las estimaciones de los coeficientes por MCO, podemos formular la siguiente hipótesis nula y alternativa para probar si la longitud de la aleta tiene un Estadísticamente significante impacto en la Masa Corporal:

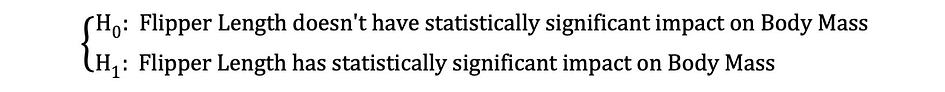
donde H0 y H1 representan la Hipótesis Nula y la Hipótesis Alternativa, respectivamente. Rechazar la hipótesis nula significaría que un aumento de una unidad en Longitud de la aleta tiene un impacto directo en la Masa Corporal. Dado que la estimación del parámetro de ?1 describe este impacto de la variable independiente, Longitud de la aleta, en la variable dependiente, Masa corporal. Esta hipótesis se puede reformular de la siguiente manera:

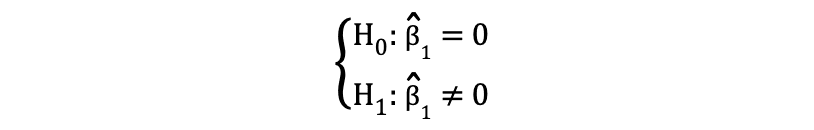
donde H0 establece que la estimación del parámetro de ?1 es igual a 0, es decir Longitud de la aleta en efecto Masa Corporal is Estadísticamente insignificante mientras H0 establece que la estimación del parámetro de ?1 no es igual a 0, lo que sugiere que Longitud de la aleta en efecto Masa Corporal is Estadísticamente significante.

Errores tipo I y tipo II

Al realizar la prueba de hipótesis estadística, es necesario considerar dos tipos conceptuales de errores: error de tipo I y error de tipo II. El error de tipo I ocurre cuando la hipótesis nula se rechaza incorrectamente, mientras que el error de tipo II ocurre cuando la hipótesis nula no se rechaza incorrectamente. una confusión matriz puede ayudar a visualizar claramente la gravedad de estos dos tipos de errores.

Como regla general, los estadísticos tienden a poner la versión de la hipótesis bajo el Hipótesis nula esa eso hay que rechazarlo, Considerando que la versión aceptable y deseada se indica bajo el Hipótesis alternativa.

Una vez que se establecen las hipótesis nula y alternativa y se definen los supuestos de la prueba, el siguiente paso es determinar qué prueba estadística es apropiada y calcular la Estadística de prueba. Se puede determinar si se rechaza o no el Nulo comparando el estadístico de prueba con el valor crítico. Esta comparación muestra si el estadístico de prueba observado es más extremo que el valor crítico definido y puede tener dos posibles resultados:

• ¿El estadístico de prueba es más extremo que el valor crítico? la hipótesis nula puede ser rechazada
• ¿La estadística de prueba no es tan extrema como el valor crítico? no se puede rechazar la hipotesis nula

El valor crítico se basa en un valor predeterminado Nivel significativo ? (usualmente elegido para ser igual al 5%) y el tipo de distribución de probabilidad que sigue la estadística de prueba. El valor crítico divide el área bajo esta curva de distribución de probabilidad en el regiones de rechazo y región de no rechazo. Hay numerosas pruebas estadísticas utilizadas para probar varias hipótesis. Ejemplos de pruebas estadísticas son prueba t de Student, Prueba F, Prueba de chi-cuadrado, Prueba de endogeneidad de Durbin-Hausman-Wu, White Prueba de heterocedasticidad. En este artículo, veremos dos de estas pruebas estadísticas.

El error de tipo I ocurre cuando la hipótesis nula se rechaza incorrectamente, mientras que el error de tipo II ocurre cuando la hipótesis nula no se rechaza incorrectamente.

prueba t de Student

Una de las pruebas estadísticas más simples y populares es la prueba t de Student. que se puede usar para probar varias hipótesis, especialmente cuando se trata de una hipótesis donde el área principal de interés es encontrar evidencia del efecto estadísticamente significativo de un variable única. El las estadísticas de prueba de la prueba t siguen Distribución t de Student y se puede determinar de la siguiente manera:

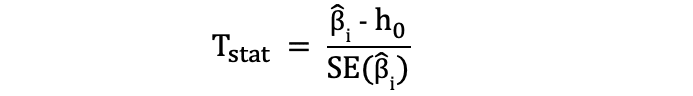
donde h0 en el denominador es el valor contra el cual se prueba la estimación del parámetro. Entonces, las estadísticas de la prueba t son iguales a la estimación del parámetro menos el valor hipotético dividido por el error estándar de la estimación del coeficiente. En la hipótesis establecida anteriormente, en la que queríamos probar si la longitud de la aleta tiene un impacto estadísticamente significativo en la masa corporal o no. Esta prueba se puede realizar mediante una prueba t y, en ese caso, h0 es igual a 0, ya que la estimación del coeficiente de pendiente se prueba contra el valor 0.

Hay dos versiones de la prueba t: una prueba t de dos caras y prueba t unilateral. Si necesita la primera o la última versión de la prueba depende completamente de la hipótesis que desea probar.

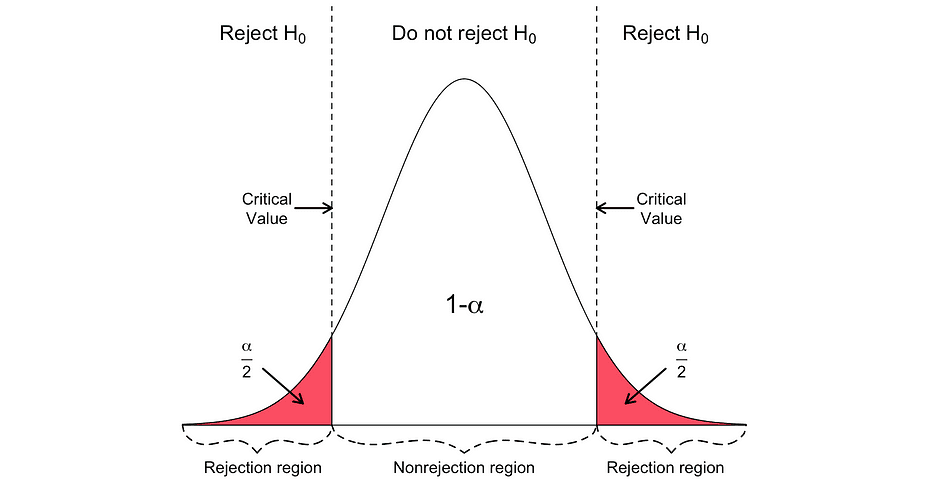
el de dos caras or prueba t de dos colas se puede utilizar cuando la hipótesis está probando igual   no es igual relación bajo las Hipótesis Nula y Alternativa que es similar al siguiente ejemplo:

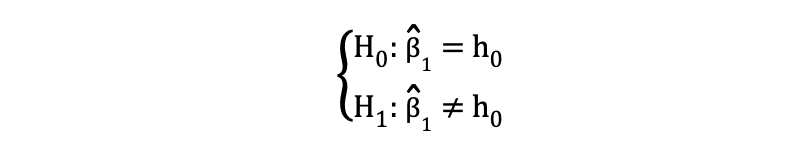
La prueba t de dos caras tiene dos regiones de rechazo como se visualiza en la siguiente figura:

Fuente de imagen: Hartmann, K., Krois, J., Waske, B. (2018): E-Learning Project SOGA: Estadísticas y análisis de datos geoespaciales. Departamento de Ciencias de la Tierra, Freie Universitaet Berlin

En esta versión de la prueba t, el Nulo se rechaza si las estadísticas t calculadas son demasiado pequeñas o demasiado grandes.

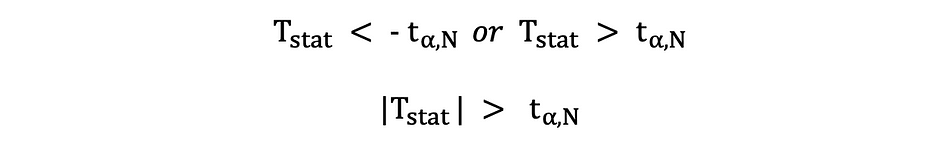
Aquí, las estadísticas de la prueba se comparan con los valores críticos según el tamaño de la muestra y el nivel de significancia elegido. Para determinar el valor exacto del punto de corte, la tabla de distribución t bilateral puede ser usado.

El unilateral o prueba t de una cola se puede utilizar cuando la hipótesis está probando positivo negativo   negativo positivo relación bajo las Hipótesis Nula y Alternativa que es similar a los siguientes ejemplos:

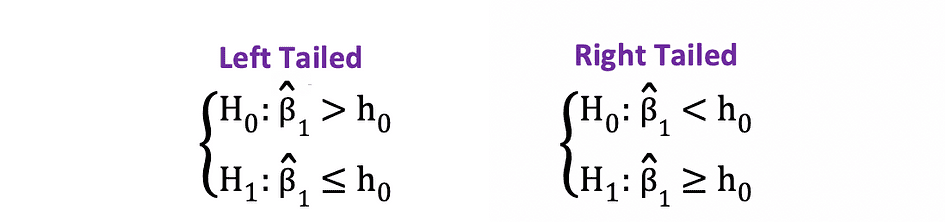
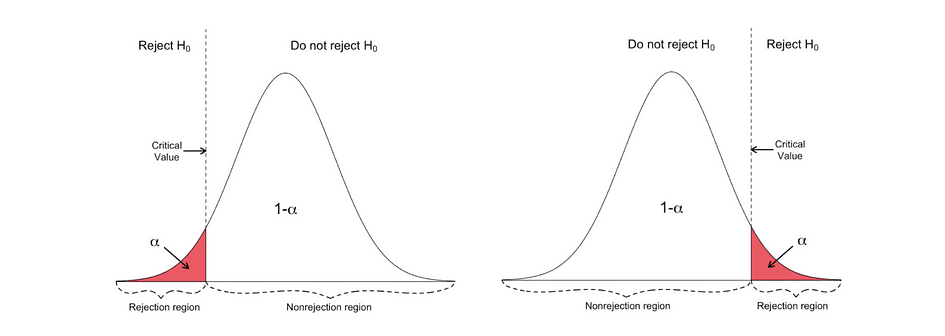
La prueba t unilateral tiene una soltero región de rechazo y dependiendo en el lado de la hipótesis, la región de rechazo está en el lado izquierdo o en el lado derecho, como se muestra en la siguiente figura:

Fuente de imagen: Hartmann, K., Krois, J., Waske, B. (2018): E-Learning Project SOGA: Estadísticas y análisis de datos geoespaciales. Departamento de Ciencias de la Tierra, Freie Universitaet Berlin

En esta versión de la prueba t, el Nulo se rechaza si la estadística t calculada es menor/mayor que el valor crítico.

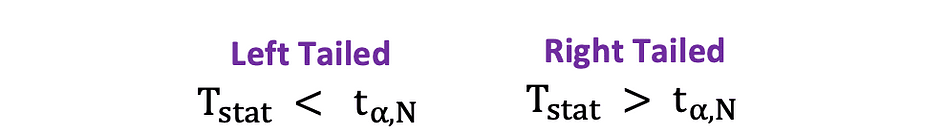
Prueba F

La prueba F es otra prueba estadística muy popular que se usa a menudo para probar hipótesis. a significación estadística conjunta de múltiples variables. Este es el caso cuando desea probar si múltiples variables independientes tienen un impacto estadísticamente significativo en una variable dependiente. El siguiente es un ejemplo de una hipótesis estadística que se puede probar usando la prueba F:

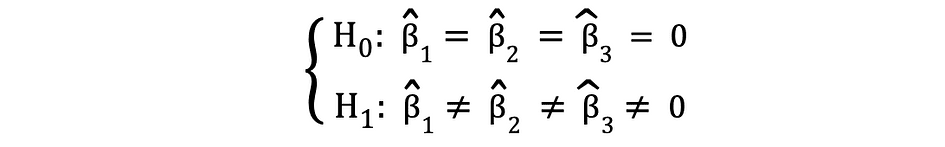
donde la Nula establece que las tres variables correspondientes a estos coeficientes son estadísticamente insignificantes en conjunto y la Alternativa establece que estas tres variables son estadísticamente significativas en conjunto. Las estadísticas de prueba de la prueba F siguen Distribución F y se puede determinar de la siguiente manera:

donde está restringido el SSR las suma de residuos al cuadrado de las límite modelo que es el mismo modelo que excluye de los datos las variables objetivo declaradas como insignificantes bajo el Nulo, el SSRunrestricted es la suma de los residuos cuadrados de la irrestricto modelo que es el modelo que incluye todas las variables, q representa el número de variables que se prueban conjuntamente para la insignificancia bajo Nulo, N es el tamaño de la muestra y k es el número total de variables en el modelo sin restricciones. Los valores de SSR se proporcionan junto a las estimaciones de los parámetros después de ejecutar la regresión OLS y lo mismo se aplica a las estadísticas F. A continuación se muestra un ejemplo de salida del modelo MLR en el que se marcan los valores SSR y F-statistics.

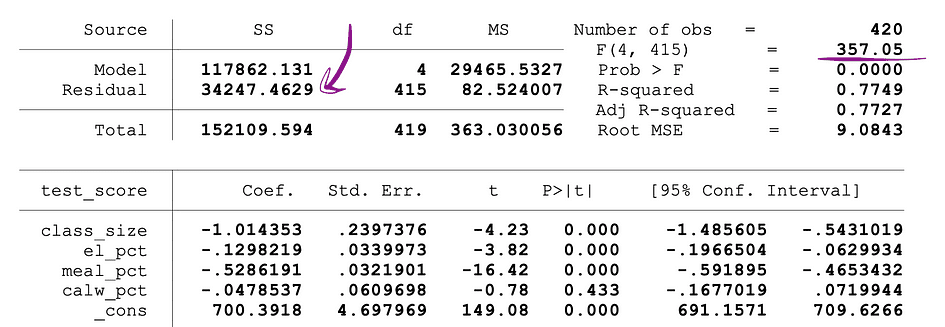
Fuente de imagen: acciones y whatson

La prueba F tiene una sola región de rechazo como se visualiza a continuación:

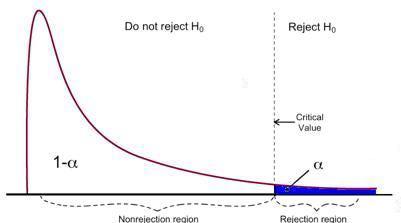
Fuente de imagen: U de Michigan

Si las estadísticas F calculadas son mayores que el valor crítico, entonces se puede rechazar el Nulo, lo que sugiere que las variables independientes son estadísticamente significativas en conjunto. La regla de rechazo se puede expresar de la siguiente manera:

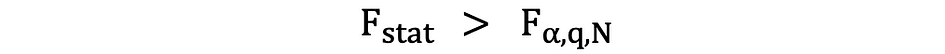
Otra forma rápida de determinar si rechazar o apoyar la hipótesis nula es mediante el uso de valores p. El valor p es la probabilidad de que ocurra la condición bajo Nulo. Dicho de otra manera, el valor p es la probabilidad, suponiendo que la hipótesis nula sea verdadera, de observar un resultado al menos tan extremo como el estadístico de prueba. Cuanto más pequeño es el valor p, más fuerte es la evidencia en contra de la hipótesis nula, lo que sugiere que puede rechazarse.

La interpretación de un p-el valor depende del nivel de significación elegido. En la mayoría de los casos, se utilizan niveles de significación del 1 %, 5 % o 10 % para interpretar el valor p. Entonces, en lugar de usar la prueba t y la prueba F, los valores p de estas estadísticas de prueba se pueden usar para probar las mismas hipótesis.

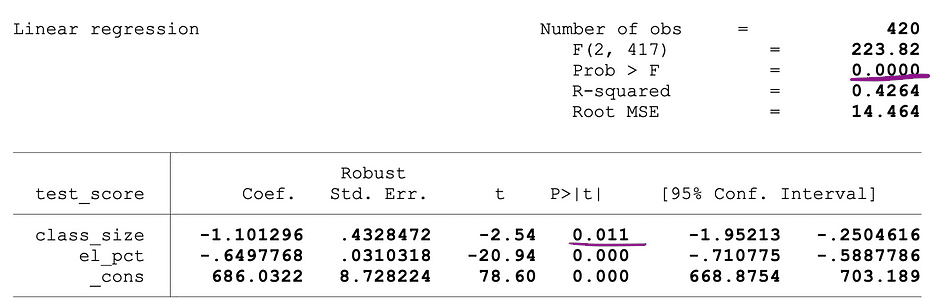
La siguiente figura muestra un resultado de muestra de una regresión OLS con dos variables independientes. En esta tabla, el valor p de la prueba t, que prueba la significación estadística de tamaño de la clase estimación del parámetro de la variable, y el valor p de la prueba F, probando la significación estadística conjunta de la tamaño de la clase, y el_pct Las estimaciones de los parámetros de las variables están subrayadas.

Fuente de imagen: acciones y whatson

El valor p correspondiente a la tamaño de la clase variable es 0.011 y al comparar este valor con los niveles de significación 1% o 0.01, 5% o 0.05, 10% o 0.1, se pueden sacar las siguientes conclusiones:

• 0.011 > 0.01 ? El valor nulo de la prueba t no se puede rechazar con un nivel de significancia del 1 %.
• 0.011 < 0.05 ? El valor nulo de la prueba t se puede rechazar con un nivel de significación del 5 %
• 0.011 < 0.10 ?El valor nulo de la prueba t se puede rechazar con un nivel de significancia del 10 %

Entonces, este valor p sugiere que el coeficiente de la tamaño de la clase variable es estadísticamente significativa a niveles de significancia del 5% y 10%. El valor p correspondiente a la prueba F es 0.0000 y dado que 0 es menor que los tres valores de corte; 0.01, 0.05, 0.10, podemos concluir que el Nulo de la prueba F puede rechazarse en los tres casos. Esto sugiere que los coeficientes de tamaño de la clase y el_pct las variables son conjuntamente estadísticamente significativas a niveles de significancia del 1%, 5% y 10%.

Limitación de los valores de p

Aunque el uso de valores p tiene muchos beneficios, pero también tiene limitaciones.. Es decir, el valor p depende tanto de la magnitud de la asociación como del tamaño de la muestra. Si la magnitud del efecto es pequeña y estadísticamente insignificante, el valor p aún podría mostrar una Impacto significativo porque el tamaño de muestra grande es grande. También puede ocurrir lo contrario, un efecto puede ser grande, pero no cumplir con los criterios de p<0.01, 0.05 o 0.10 si el tamaño de la muestra es pequeño.

La estadística inferencial utiliza datos de muestra para hacer juicios razonables sobre la población de la que se originaron los datos de muestra. Se utiliza para investigar las relaciones entre las variables dentro de una muestra y hacer predicciones sobre cómo estas variables se relacionarán con una población más grande.

Ambos Ley de los Grandes Números (LLN) y Teorema del límite central (CLM) tienen un papel importante en las estadísticas inferenciales porque muestran que los resultados experimentales se mantienen independientemente de la forma que tenía la distribución de la población original cuando los datos son lo suficientemente grandes. Cuantos más datos se recopilan, más precisas se vuelven las inferencias estadísticas y, por lo tanto, se generan estimaciones de parámetros más precisas.

Ley de los Grandes Números (LLN)

Suponer X1, X2, . . . , xn son todas las variables aleatorias independientes con la misma distribución subyacente, también llamadas independientes distribuidas idénticamente o iid, donde todas las X tienen la misma media ? y desviación estándar ?. A medida que crece el tamaño de la muestra, ¿la probabilidad de que el promedio de todas las X sea igual a la media? es igual a 1. La Ley de los Grandes Números se puede resumir de la siguiente manera:

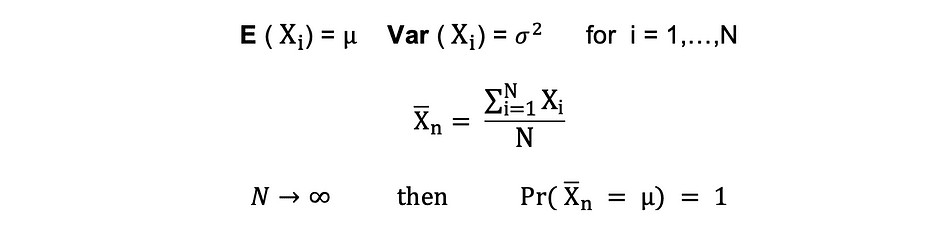
Teorema del límite central (CLM)

Suponer X1, X2, . . . , xn son todas las variables aleatorias independientes con la misma distribución subyacente, también llamadas independientes distribuidas idénticamente o iid, donde todas las X tienen la misma media ? y desviación estándar ?. A medida que crece el tamaño de la muestra, la distribución de probabilidad de X converge en la distribución en distribución Normal con media ? y varianza ?-al cuadrado El teorema del límite central se puede resumir de la siguiente manera:

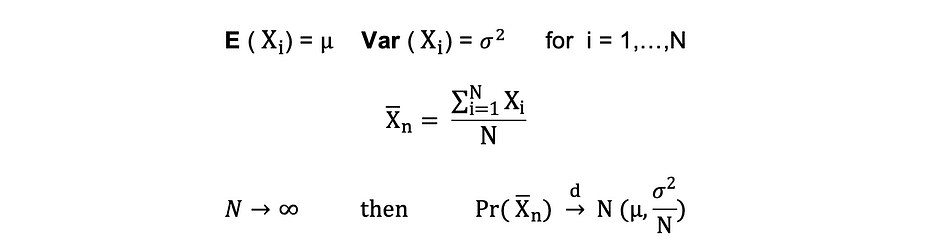
Dicho de otra manera, cuando tienes una población con media? y la desviación estándar? y toma muestras aleatorias lo suficientemente grandes de esa población con reemplazo, entonces la distribución de las medias muestrales se distribuirá aproximadamente normalmente.

La reducción de la dimensionalidad es la transformación de los datos de un espacio de alta dimensión post-extracción espacio de baja dimensión de modo que esta representación de baja dimensión de los datos aún contenga las propiedades significativas de los datos originales tanto como sea posible.

Con el aumento de la popularidad de Big Data, también aumentó la demanda de estas técnicas de reducción de dimensionalidad, reduciendo la cantidad de datos y características innecesarias. Ejemplos de técnicas populares de reducción de dimensionalidad son Análisis de componentes principales, Análisis factorial, Correlación canónica, Bosque al azar.

Análisis de los componentes Principio (PCA)

El análisis de componentes principales o PCA es una técnica de reducción de la dimensionalidad que se usa muy a menudo para reducir la dimensionalidad de grandes conjuntos de datos, mediante la transformación de un gran conjunto de variables en un conjunto más pequeño que todavía contiene la mayor parte de la información o la variación en el gran conjunto de datos original. .

Supongamos que tenemos un dato X con p variables; X1, X2, …., Xp con vectores propios e1, …, ep, y valores propios ?1,…, ?pág. Los valores propios muestran la varianza explicada por un campo de datos particular de la varianza total. La idea detrás de PCA es crear nuevas variables (independientes), llamadas componentes principales, que son una combinación lineal de la variable existente. el yoth componente principal se puede expresar de la siguiente manera:

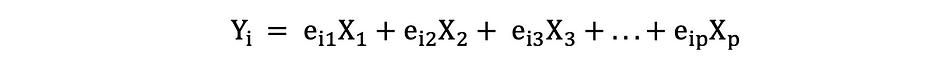
Luego, utilizando Regla del codo or Regla de Káiser, puede determinar el número de componentes principales que resumen de forma óptima los datos sin perder demasiada información. También es importante mirar la proporción de la variación total (PRTV) que se explica por cada componente principal para decidir si conviene incluirlo o excluirlo. PRTV para la ith componente principal se puede calcular utilizando valores propios de la siguiente manera:

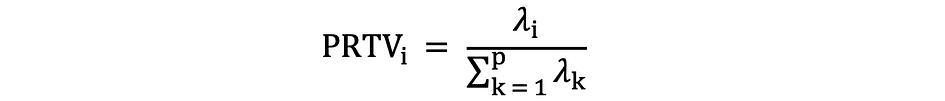
Regla del codo

La regla del codo o el método del codo es un enfoque heurístico que se utiliza para determinar el número de componentes principales óptimos a partir de los resultados de PCA. La idea detrás de este método es trazar la variación explicada en función del número de componentes y tomar el codo de la curva como el número de componentes principales óptimos. A continuación, se muestra un ejemplo de un gráfico de dispersión de este tipo en el que el PRTV (eje Y) se representa en el número de componentes principales (eje X). El codo corresponde al valor 2 del eje X, lo que sugiere que el número de componentes principales óptimos es 2.

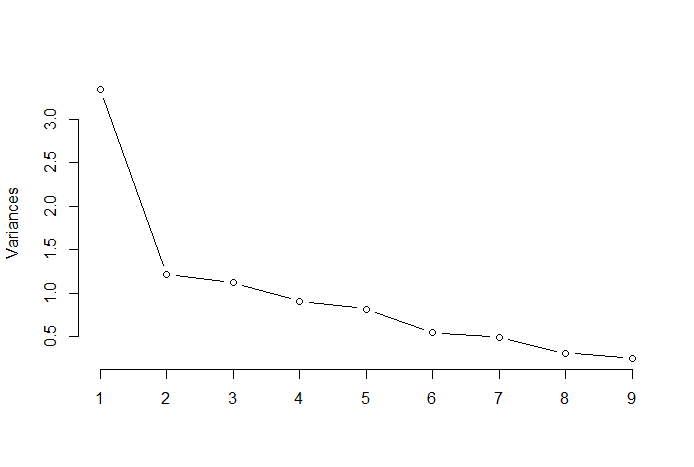
Fuente de imagen: Estadísticas multivariadas Github

Análisis factorial (AF)

El análisis factorial o FA es otro método estadístico para la reducción de la dimensionalidad. Es una de las técnicas de interdependencia más utilizadas y se utiliza cuando el conjunto relevante de variables muestra una interdependencia sistemática y el objetivo es descubrir los factores latentes que crean una similitud. Supongamos que tenemos un dato X con p variables; X1, X2, …., Xp. El modelo FA se puede expresar de la siguiente manera:

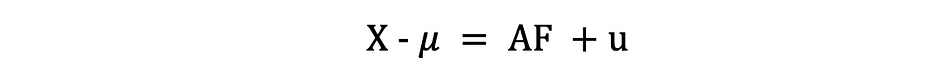
donde X es una matriz [px N] de p variables y N observaciones, µ es [px N] matriz media poblacional, A es [pxk] común matriz de cargas factoriales, F [kx N] es la matriz de factores comunes y u [pxN] es la matriz de factores específicos. Entonces, dicho de otra manera, un modelo factorial es como una serie de regresiones múltiples, prediciendo cada una de las variables Xi a partir de los valores de los factores comunes no observables fi:

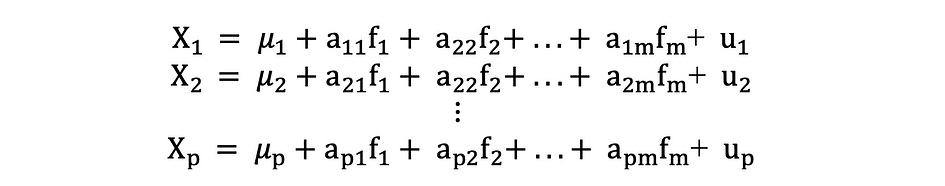
Cada variable tiene k de sus propios factores comunes, y estos están relacionados con las observaciones a través de la matriz de carga factorial para una sola observación de la siguiente manera: En el análisis factorial, el factores importantes se calculan para maximizarán varianza entre grupos mientras minimizando la variación en el grupoe. Son factores porque agrupan las variables subyacentes. A diferencia de PCA, en FA los datos deben normalizarse, dado que FA asume que el conjunto de datos sigue una distribución normal.

 
 
Tatev Karen Aslanian es un científico de datos de pila completa experimentado con un enfoque en el aprendizaje automático y la IA. También es cofundadora de tecnología lunar, una plataforma educativa de tecnología en línea y creadora de The Ultimate Data Science Bootcamp. Tatev Karen, con una licenciatura y una maestría en econometría y ciencias de la gestión, ha crecido en el campo del aprendizaje automático y la inteligencia artificial, centrándose en sistemas de recomendación y PNL, con el apoyo de su investigación científica y artículos publicados. Después de cinco años de enseñanza, Tatev ahora está canalizando su pasión hacia LunarTech, ayudando a dar forma al futuro de la ciencia de datos.

 
Original. Publicado de nuevo con permiso.
 

• Distribución de relaciones públicas y contenido potenciado por SEO. Consiga amplificado hoy.
• PlatoData.Network Vertical Generativo Ai. Empodérate. Accede Aquí.
• PlatoAiStream. Inteligencia Web3. Conocimiento amplificado. Accede Aquí.
• PlatoESG. Automoción / vehículos eléctricos, Carbón, tecnología limpia, Energía, Ambiente, Solar, Gestión de residuos. Accede Aquí.
• Desplazamientos de bloque. Modernización de la propiedad de compensaciones ambientales. Accede Aquí.
• Fuente: https://www.kdnuggets.com/2023/08/fundamentals-statistics-data-scientists-analysts.html?utm_source=rss&utm_medium=rss&utm_campaign=fundamentals-of-statistics-for-data-scientists-and-analysts